Capítulo 4 Teste-t

Ao iniciarmos nossos estudos geralmente estamos interessados em saber se alguma característica da população que coletamos e analisamos é similar a uma outra população. Podemos abordar essa ideia por diversos caminhos porém vamos iniciar essas análises em R através do teste-t para uma amostra e a discussão sobre hipótese nula, caudalidade e nível de confiança. A partir de então seguiremos para o teste-t com duas amostras e o teste-t pareado.

4.1 Teste-t para uma amostra

Conduzimos esse teste quando objetivamos verificar se a média de uma dada variável é similar a um valor esperado. Ao falarmos de média percebemos que a variável com a qual estamos lidando é do tipo númerica ou inteiro (a diferença entre ambas consiste na presença de casas decimais, na variável númerica), ou seja, mensurável (= quantitativo). Ao compararmos a média de nossa variável a um valor previamente estipulado duas hipóteses são naturalmente construídas, a hipótese nula (H0) e a hipótese alternativa (HA) (Tabela 4.1).

Tabela 4.1: Principais características do teste-t para uma amostra

Atributos	Características
Tipo de variável	Quantitativa
Quantidade de variáveis	1
Hipótese nula	A média da variável é similar ao valor previamente estipulado
Fórmula	\[t=\frac{(\overline{X}-\mu)}{(s/sqrt(N))}\] Onde, \(\overline{X}\): média da amostra, \(\mu\): média teórica esperada, s: desvio padrão da amostra e N: tamanho da amostra.
Observação	Não há a necessidade de post-hoc nem expressa-la graficamente

Caso você ainda não tenha seus dados, vamos verificar como conduzir o teste-t por meio de exemplos utilizando valores fictícios.

Imagine o seguinte exemplo: 100 camarões foram coletados em um estuário. Suas medidas em relação ao tamanho foram tomadas e deseja-se saber se o seu tamanho médio é similar ou não ao tamanho médio (25,80mm) da mesma espécie, observada em outro estuário.

A partir do exemplo acima podemos definir nossas hipóteses, onde.

• H0: média observada é igual à média esperada;
• HA: média observada é diferente da média esperada;

Vamos começar gerando os dados relativos ao tamanho observado dos camarões que coletamos.

Para isso vamos utilizar a função set.seed() que define os números aleatórios que serão gerados. Dessa forma, quando aplicado essa função associada a um número comum, no caso “1234”, os números aleatórios que você irá gerar para o objeto tamanho.camarao, por exemplo, serão os mesmos dos apresentados aqui.

A nossa segunda linha de comando utilizará a função rnorm() o qual gera números aleatórios considerando uma distribuição normal e soma esses valores gerados a uma distribuição uniforme gerada pela função runif(). A estas funções adicionamos argumentos que definem a quantidade de números gerados (argumento “n”), o valor mínimo que pode ser gerado (argumento “min”) e o valor máximo que pode ser gerado (argumento “max”). E guardamos o resultado obtido em um objeto chamado tamanho.camarao. Relembre que o nome do objeto não deve apresentar espaços ou acentos, que pode gerar problemas e/ou dificuldades na condução das análises.

set.seed(1234)
tamanho.camarao <- rnorm(n = 100) + runif(n = 100, min = 17, max = 33)

Vamos verificar o resultado. Basta digitarmos o nome do objeto.

tamanho.camarao

##   [1] 26.36501 25.73118 23.16434 26.93999 25.85006 29.22289 21.34791 22.92014
##   [9] 19.70599 31.88009 25.58378 20.48762 19.18464 29.19344 27.02799 31.80449
##  [17] 26.70808 27.30077 23.83039 33.02083 23.89138 17.01159 20.68980 22.81711
##  [25] 18.44307 23.54454 30.40893 21.37080 25.12759 23.97507 30.85514 25.59575
##  [33] 17.99771 29.42112 24.44470 19.22824 26.81323 20.57450 24.53800 32.36946
##  [41] 25.23524 19.84181 19.61879 27.74526 31.68906 23.66401 28.26906 24.93702
##  [49] 31.93121 29.25393 23.70445 25.96390 20.11329 20.45772 17.87934 26.57236
##  [57] 22.84551 16.27916 28.03817 24.16301 31.17074 20.02190 26.56155 20.62508
##  [65] 18.92214 20.38837 27.83197 18.62320 19.12094 29.29845 22.72270 28.68786
##  [73] 22.64878 30.43969 19.48136 24.94834 28.74896 24.99252 21.52521 22.19714
##  [81] 22.72903 23.69804 30.32393 29.37573 29.65554 22.18997 24.85922 21.19787
##  [89] 27.94906 28.93757 27.42930 23.87127 33.93523 21.89126 26.24338 29.48277
##  [97] 26.96407 19.72505 28.14750 24.06552

Vamos observar as métricas e gráficos, conforme já fizemos nos capítulos anteriores, mas relativos ao objeto criado.

mean(tamanho.camarao)

## [1] 24.86218

min(tamanho.camarao)

## [1] 16.27916

max(tamanho.camarao)

## [1] 33.93523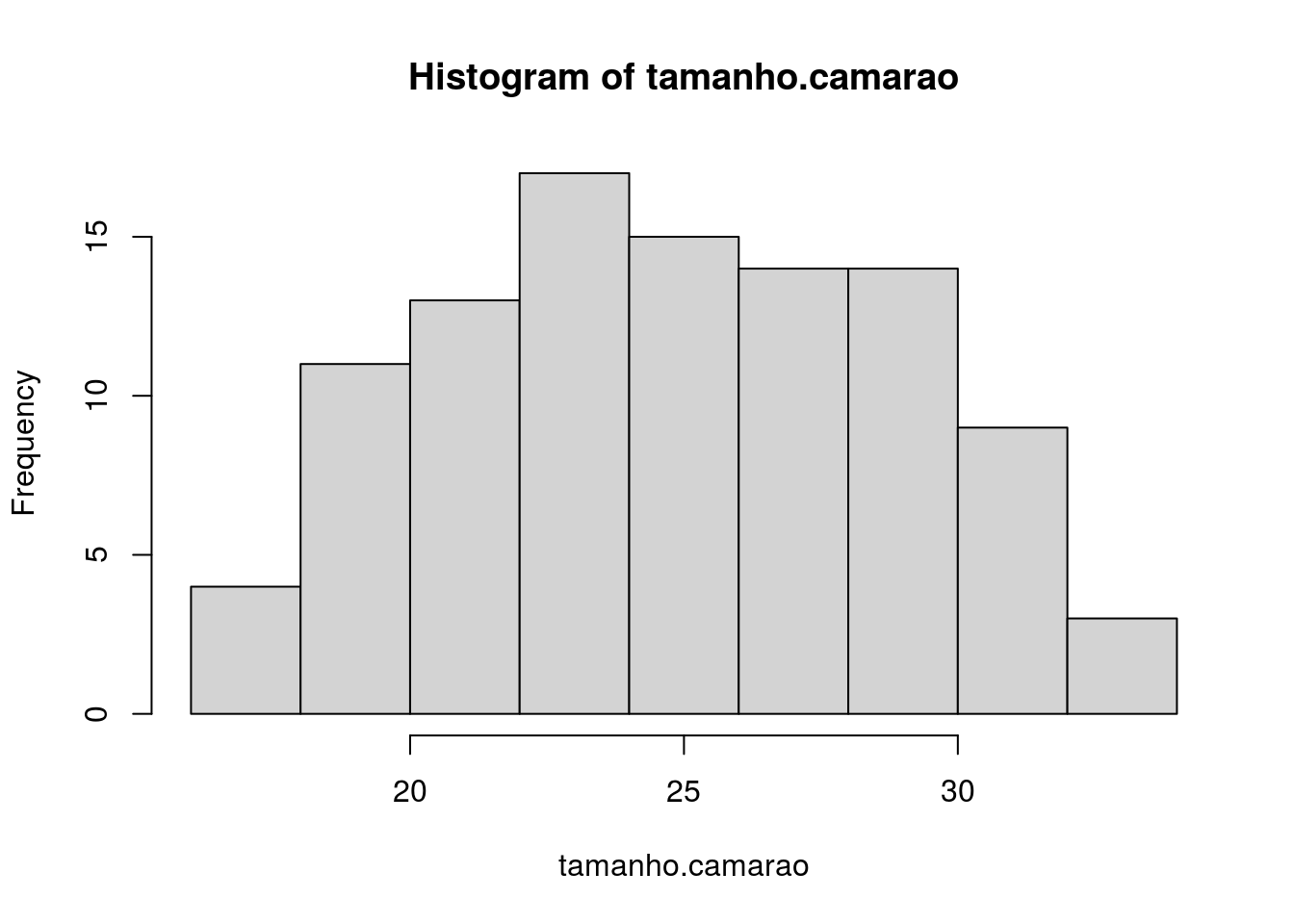

length(tamanho.camarao)

## [1] 100

hist(tamanho.camarao)

Figura 4.1: Histograma dos valores do objeto relativo ao tamanho dos camarões

Como podemos ver os valores mínimo e máximo são similares ao que definimos e o número de elementos é o mesmo. Graficamente podemos ver que a distribuição é normal, pois como vimos utilizamos uma função que cria uma distribuição normal com limites definidos pela função runif(). Além disso vemos que há uma maior frequência dos valores em torno de 25 (Figura 4.1).

Vamos verificar se esse valor que geramos (obtivemos de tamanho do camarão) são similares ao observado em outra localidade, por meio do teste-t para uma amostra. Para isso imaginemos que o valor médio esperado para o tamanho desta espécie de camarão em outra localidade é de 25,80mm. Para isso iremos criar o objeto esperado que contem esse valor.

esperado = 25.80

Agora vamos, por meio da função t.test() realizar o teste-t para verificar se os nossos dados tem média similar ao esperado.

t.test(x = tamanho.camarao, mu = esperado)

## 
##  One Sample t-test
## 
## data:  tamanho.camarao
## t = -2.2432, df = 99, p-value = 0.02711
## alternative hypothesis: true mean is not equal to 25.8
## 95 percent confidence interval:
##  24.03263 25.69173
## sample estimates:
## mean of x 
##  24.86218

O primeiro argumento da função t.test(): “x” refere-se ao nosso objeto que contem os dados referentes ao tamanho que coletamos (tamanho.camarao) e o segundo argumento “mu” refere-se ao objeto que contem a média do tamanho obtido em outro estuário (esperado).

Conforme podemos visualizar no resultado temos 9 linhas. A primeira linha nos diz qual teste está sendo conduzido, neste caso é (One Sample t-test ou teste-t para uma amostra), a segunda linha nos retorna o conjunto de dados que utilizamos, a terceira linha nos retorna o valor do teste-t (t = -2,2432) o grau de liberdade (df = 99) e o valor de probabilidade associado ao teste (p-value = 0,02711), a quarta linha nos retorna qual é nossa hipótese alternativa, caso a aceitemos (a qual nos diz que: a média dos nossos dados não é igual à 25,8), a quinta e sexta linhas nos fornece o intervalo de confiança de 95% dos nossos dados (24,03263 e 25,69173) e da sétima a nona linha refere-se a informação relativa a média dos nossos dados (24,86218).

Em resumo, podemos inferir que a média dos nossos dados é diferente do valor esperado pois o p-value foi menor que 0,05. Detalhadamente podemos dizer que: a média do tamanho dos camarões que coletamos (24,86 mm) é estatisticamente menor do que a média presente no outro estuário (25,80 mm) a um nível de confiança de 95%, portanto rejeitamos H0.

Ok, verificamos e entendemos como conduzir a análise. Mas há um conceito estatístico importante na análise do teste-t, a caudalidade. No exemplo anterior nós trabalhamos com as hipóteses de que a média de um conjunto de dados é igual (H0) ou diferente (HA) da média esperada. O que implica em dizer que a média que observamos pode ser maior ou menor do que o esperado. Contudo em algumas instâncias podemos querer verificar se a média do nosso conjunto de dados é maior ou igual ou menor ou igual a média esperada e não diferente. Desta diferença na construção da hipótese que emerge o conceito da caudalidade. No exemplo anterior foi testado a hipótese bicaudal que é tido como padrão (default) na função do R que executamos.

A diferença do teste-t bicaudal para o unicaudal depende da pergunta e hipótese levantada previamente. Então antes de realizar este teste mantenha-se atento ao que se deseja testar.

Vejamos o seguinte exemplo: Em um costão rochoso foi observado ao longo do “dia 1” 100 estrelas do mar em diferentes alturas, em relação a baixamar. Essas alturas foram mensuradas (valores serão construídos abaixo no objeto denominado estrela). Sabe-se que no dia anterior “dia 0” a altura média das estrelas no mesmo costão foi de 0,90m. Sabe-se também que o “dia 0” foi mais frio e que dias mais frios implicam em maiores alturas.

Neste exemplo estamos interessado em saber se a altura das estrelas do mar no “dia 1” é menor que a do “dia 0”, visto que o “dia 1” é mais quente.

A partir dessas informações podemos construir as seguintes hipóteses:

• H0: A média da altura das estrelas do mar no dia 1 é maior ou igual ao dia 0;
• HA: A média da altura das estrelas do mar no dia 1 é menor que a do dia 0;

Matematicamente podemos escrever as hipóteses da seguinte forma:

• H0: \(\mu_{dia.1} \geq \mu_{dia.0}\)
• HA: \(\mu_{dia.1} < \mu_{dia.0}\)

De maneira similar ao exemplo anterior vamos gerar nosso conjunto de dados que contêm os valores de altura das estrelas do mar no costão rochoso, a diferença é que iremos inserir o argumento “sd” na função rnorm() que corresponde ao desvio padrão (de 0,02) dos dados normais que estamos gerando e guardar esse resultado no objeto estrelas.

set.seed(1234)
estrelas <- rnorm(n = 100, sd = 0.02) + runif(n = 100, min = 0.4, max = 1.3)

Conforme também fizemos anteriormente calcularemos algumas métricas para entender os dados e um histograma básico (Figura 4.2) para visualizar a forma dos dados que representam a altura que as estrelas se encontram no ambiente.

mean(estrelas)

## [1] 0.8479302

min(estrelas)

## [1] 0.387487

max(estrelas)

## [1] 1.290766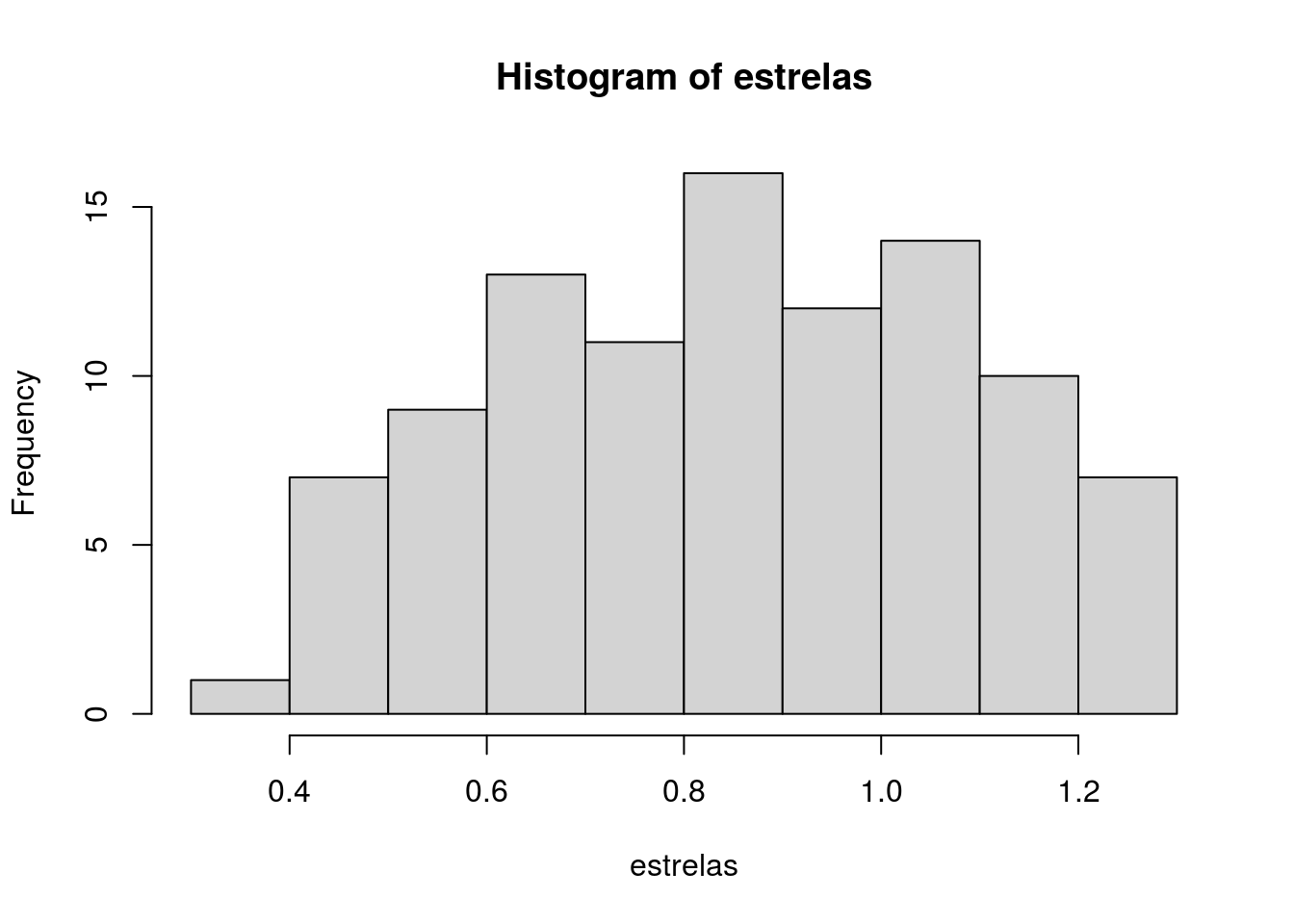

length(estrelas)

## [1] 100

hist(estrelas)

Figura 4.2: Histograma dos valores relativos a altura das estrelas do mar no costão rochoso

Agora vamos criar o objeto dia.0 que contêm o valor referente a altura das estrelas no dia 0.

dia.0 = 0.90

Agora o teste-t onde avaliaremos se a média da altura das estrelas do mar que obtivemos para o “dia 1” são maiores ou iguais ao “dia 0”, utilizando o argumento “alternative” e definido-o como less. Este argumento pode ser definido de 3 formas: two-sided que é o padrão (default), greater ou less. O argumento “alternative” seguirá o sinal da hipótese alternativa (HA) que foi construída para o teste.

t.test(x = estrelas, mu = dia.0, alternative = "less")

## 
##  One Sample t-test
## 
## data:  estrelas
## t = -2.2073, df = 99, p-value = 0.0148
## alternative hypothesis: true mean is less than 0.9
## 95 percent confidence interval:
##       -Inf 0.8870986
## sample estimates:
## mean of x 
## 0.8479302

Com isso podemos avaliar o resultado que é similar ao que vimos anteriormente com poucas mudanças. A primeira linha (One Sample t-test) informa sobre o teste realizado. A segunda linha indica o nome do conjunto de dados que inserimos. A terceira linha nos dá o valor do teste-t (t = -2,2073), do grau de liberdade (df = 99) e da probabilidade associada ao teste (p-value = 0.0148). A quarta linha indica a hipótese alternativa, caso seja aceita (o que é o caso), que é verdade que a média da altura das estrelas do mar do “dia 1” é menor que 0,90m. A quinta e sexta linha indicam o intervalo de confiança de 95% dos nossos dados (-Inf e 0,8870986). A sétima, oitava e nona linha referem-se a média do “dia 1”.

Como podemos notar pelo p-value rejeitamos nossa hipótese nula (H0). Portanto a média na altura das estrelas do mar do “dia 1” (aproximadamente 0,85m) é menor que a do dia “0” (0,90m).

Outro conceito importante de qualquer teste inferencial é o nível de confiança¹⁶. Até o presente momento consideramos o nível de confiança de 95%. Se quisermos altera-lo no teste-t devemos adicionar o argumento “conf.level” em proporção (valores entre 0 e 1). A sua alteração implica na alteração do nível de significância e consequentemente na zona de rejeição da hipótese nula. Se aumentarmos o seu valor fica mais difícil rejeitarmos a hipótese nula e se diminuirmos o seu valor fica mais fácil rejeitar a hipótese nula. Vejamos outro exemplo.

Um pesquisador avaliou o tamanho de cracas incrustadas no casco de uma embarcação. Objetivando saber se o tamanho médio de cracas difere do teórico esperado (13,5 mm) um teste-t bicaudal foi aplicado a um nível de confiança de 95% e 99%.

Vamos descrever as hipóteses e realizar a análise para ambos os níveis de confiança.

Neste caso temos as seguintes hipóteses:

• H0: O tamanho médio observado é similar ao teórico
• HA: O tamanho médio observado difere do teórico

Conforme já realizado anteriormente vamos gerar os dados iguais aos gerados aqui por meio das funções set.seed(), rnorm() e runif(), guardando o seu resultado em um objeto chamado cracase explora-los com algumas métricas estatśticas e gráficas de maneira similar ao que fizemos no exemplo anterior.

set.seed(1234)
cracas <- rnorm(n = 100, sd = 1.9) + runif(n = 100, min = 5, max = 25)
mean(cracas)

## [1] 14.72583

min(cracas)

## [1] 3.596275

max(cracas)

## [1] 27.27792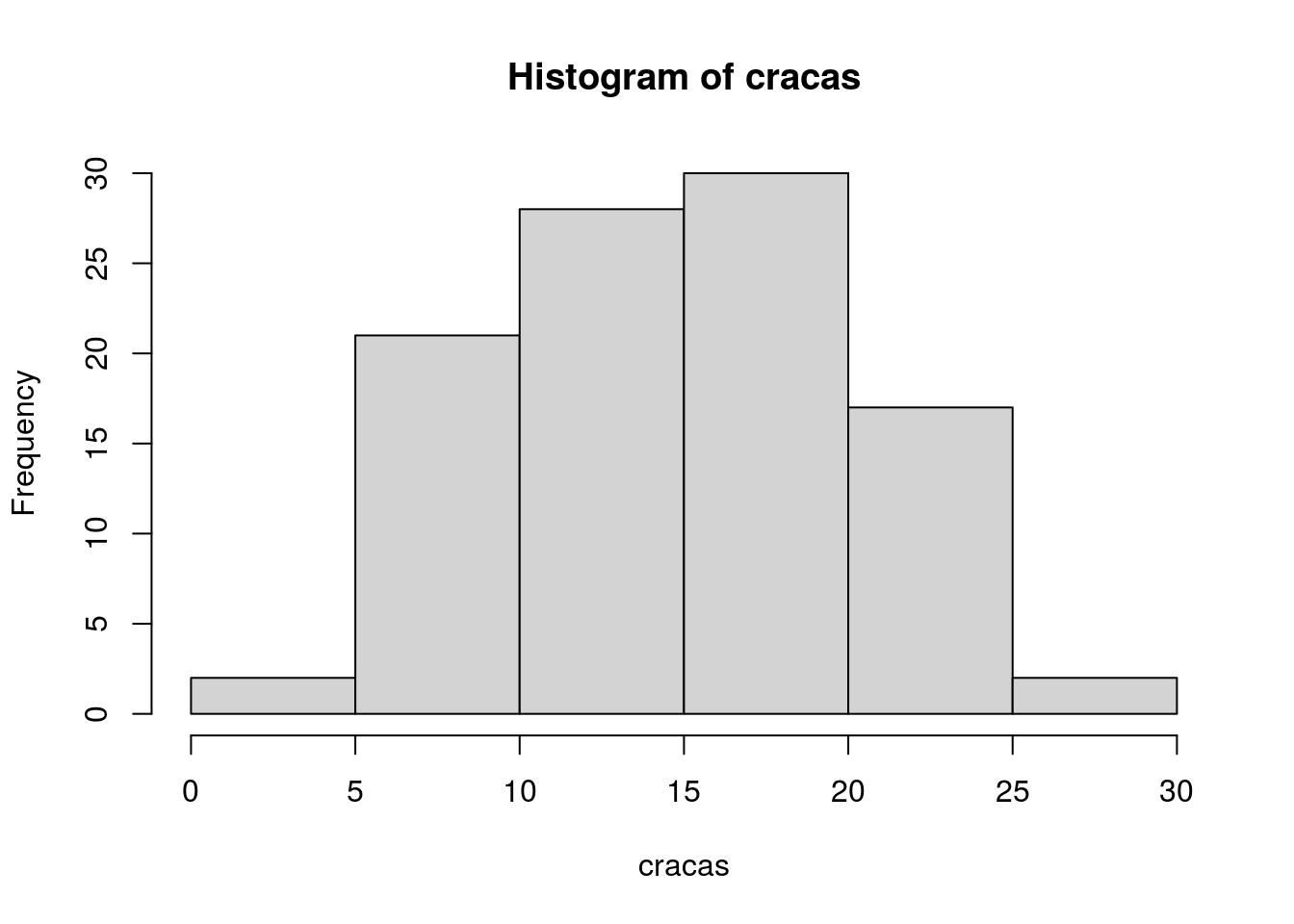

length(cracas)

## [1] 100

hist(cracas)

Figura 4.3: Histograma dos valores relativos ao tambanho das cracas incrustantes

Agora que visualizamos as métricas e graficamos os dados (Figura 4.3), sigamos construindo o objeto que guarda o valor teórico (13,5mm) e com a condução da análise.

teorico <- 13.5
t.test(x = cracas, mu = teorico, conf.level = 0.95)

## 
##  One Sample t-test
## 
## data:  cracas
## t = 2.3113, df = 99, p-value = 0.02289
## alternative hypothesis: true mean is not equal to 13.5
## 95 percent confidence interval:
##  13.67349 15.77817
## sample estimates:
## mean of x 
##  14.72583

t.test(x = cracas, mu = teorico, conf.level = 0.99)

## 
##  One Sample t-test
## 
## data:  cracas
## t = 2.3113, df = 99, p-value = 0.02289
## alternative hypothesis: true mean is not equal to 13.5
## 99 percent confidence interval:
##  13.33290 16.11876
## sample estimates:
## mean of x 
##  14.72583

Como podem ver ambos os resultados (com diferentes níveis de confiança) retornam o mesmo valor do teste-t e do p-value. E neste ponto precisamos ir com calma para evitar erro de interpretação do resultado e entender estatisticamente o que está acontencendo.

Quando representamos o nível de confiança (representado pelo argumento “conf.level”) por um valor probabilístico de 0,95 ou 0,99 estamos dizendo que o nível de significância é 0,05 e 0,01, respectivamente. Quando olhamos para o resultado do p-value, temos que levar em consideração o nível de significância.

Vejamos o nosso resultado.

No primeiro caso (“conf.level = 0.95”) temos p-value = 0,02289, como este valor é menor que 0,05 (nosso nível de significância), isso quer dizer que a média teórica está fora do intervalo de confiança dos dados, portanto rejeitamos a hipótese nula.

No segundo caso (“conf.level = 0.99”) temos o mesmo p-value (0,02289), contudo este valor é maior que nosso nível de significância (0,01), isso quer dizer que nossa média teórica está dentro do intervalo de confiança, portanto aceitamos a hipótese nula de que a média observada é similar a média teórica.

OBS: Em um primeiro momento pode parecer confuso, portanto releia o exemplo acima, assim como outras literaturas.

O nível de significância a aplicar nos seus dados depende das informações que possui sobre o organismo ou o ambiente que está estudando. Apesar da regra-de-bolso dizer 0,05 e por padrão o R definir esse nível de significância é necessário entender o que ele representa para seus dados e qual a implicação para sua hipótese e as medidas que serão tomadas. Uma dica importante é: reporte sempre o intervalo de confiança, indique o nível de significância que foi aplicado e no seu texto deixe claro o porquê de sua escolha, principalmente se for diferente do que é definido como padrão.

BÔNUS:

Embora não seja comum, podemos plotar um gráfico que represente o nosso resultado estatístico como uma curva de densidade no qual é representado o valor do teste-t, o grau de liberdade e o valor de probabilidade associado. Para isso vamos usar um pacote o qual precisa ser instalado chamado webr e precisamos carrega-lo usando a função library(). Após isso é só inserir a função que desenvolve o teste-t dentro da função plot(). Veja o resultado para ambos os níveis de confiança estabelecidos previamente.

OBS: Uma vez instalado o pacote não precisa instala-lo novamente apenas carrega-lo se estiver iniciando o R pela primeira vez.

install.packages("webr")
library(webr)

Após instalar e carregar o pacote devemos inserir o teste-t dentro da função plot(). Veja os dois exemplos abaixo.

plot(t.test(x = cracas, mu = teorico, conf.level = 0.95))

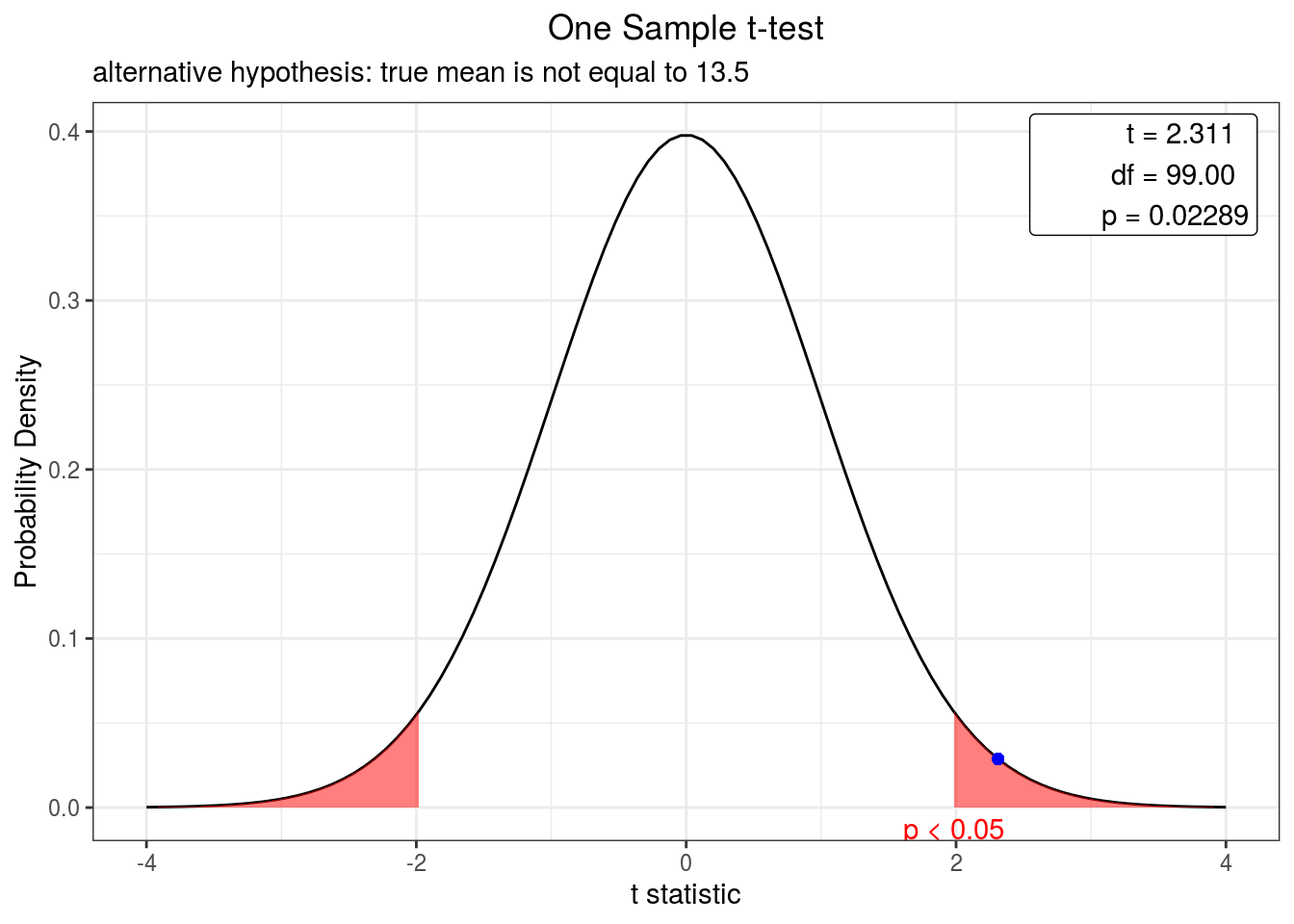
Figura 4.4: Curva de densidade representando o valor do teste-t bicaudal para o tamanho das cracas em relação a média teórica a um intervalo de confiança de 95%. O ponto azul indica o valor do teste.

plot(t.test(x = cracas, mu = teorico, conf.level = 0.99))

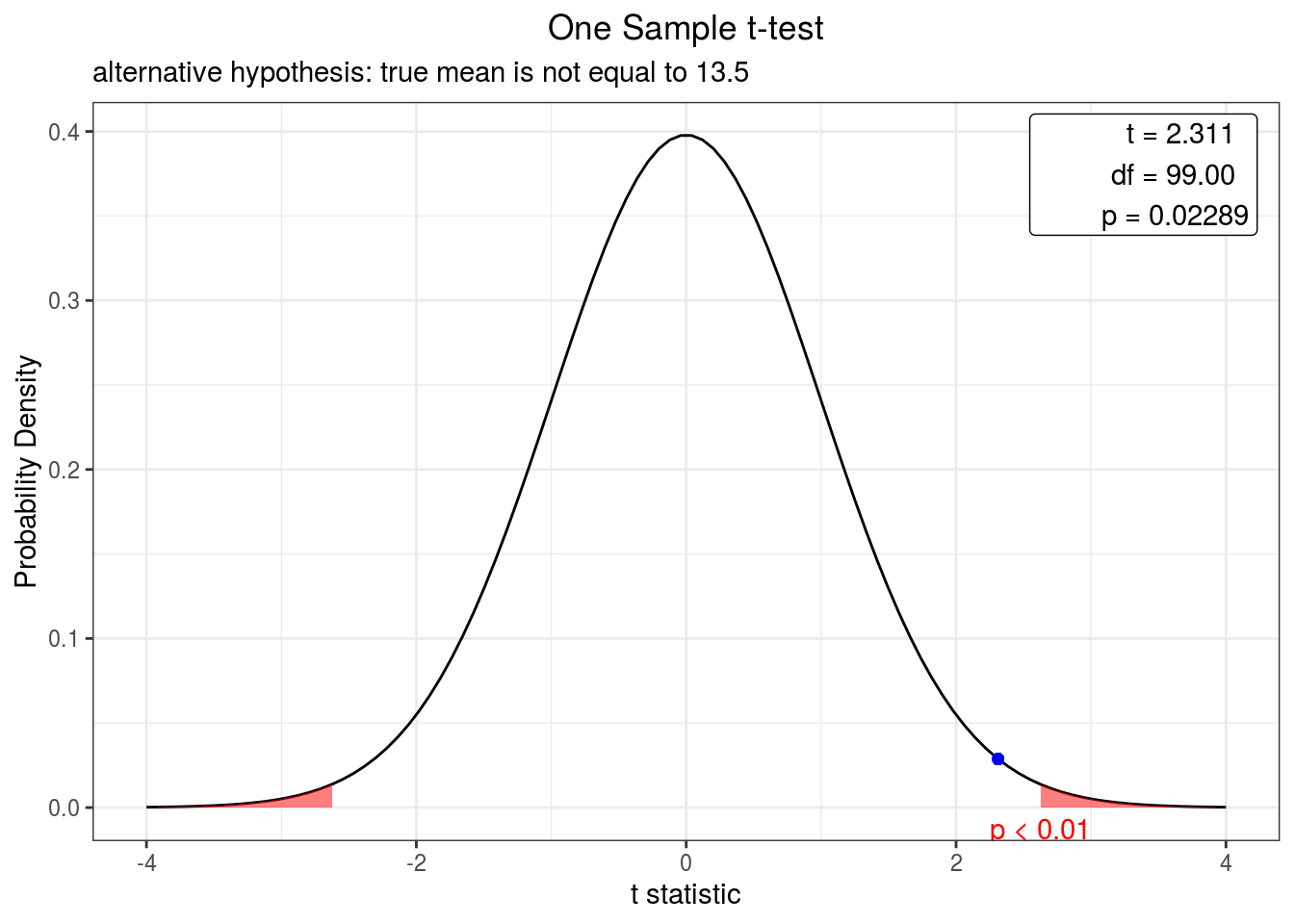
Figura 4.5: Curva de densidade representando o valor do teste-t bicaudal para o tamanho das cracas em relação a média teórica a um intervalo de confiança de 99%. O ponto azul indica o valor do teste.

Verifique que esses plots nos fornecem as curvas do teste-t os intervalos de confiança de 95% (Figura 4.4) e 99% (Figura 4.5), demarca os limites inferior e superior de vermelho e marca como ponto azul na curva de densidade o valor do teste-t associado. Como esse valor está dentro da região demarcada no intervalo de confiança de 95%, neste caso rejeitamos a hipótese nula e como no intervalo de confiança de 99% o ponto azul está fora da região demarcada aceitamos a hipótese nula.

4.2 Teste-t para duas amostras

Conduzimos esse teste quando objetivamos comparar se a média de dois grupos são similares (Tabela 4.2).

Tabela 4.2: Principais características do teste-t para duas amostras

Atributos	Características
Tipo de variável	Quantitativa e categórica
Quantidade de variáveis	2 (1 de cada tipo obrigatoriamente)
Hipótese nula	A diferença na média da variável quantitativa dos grupos é igual a 0.
Fórmula	\[t=\frac{\overline{X}_1-\overline{X}_2}{s_{\overline{X}_1-\overline{X}_2}}\], onde, \(\overline{X}_1\): média do grupo 1, \(\overline{X}_2\): média do grupo 2, s: erro padrão da diferença entre os dois grupos.
Observação	Não há a necessidade de post-hoc nem expressa-la graficamente.

Partindo desse objetivo as hipóteses nula e alternativa desse teste podem ser escritas da seguinte forma:

• H0: A diferença na média da variável quantitativa dos grupos é igual a 0;
• HA: A diferença na média da variável quantitativa dos grupos é diferente de 0;

Outra forma de apresentarmos as hipóteses relativa a este teste é:

• H0: A média da variável quantitativa é igual entre grupos;
• HA: A média da variável quantitativa é diferente entre grupos;

Outra forma de escrevermos a hipótese é em relação a caudalidade do teste e, se unicaudal, pode ser escrita da seguinte forma:

• H0: A média da variável quantitativa é maior ou igual (ou menor ou igual) entre grupos;
• HA: A média da variável quantitativa é menor (ou maior) entre grupos;

A partir desse teste, alguns pressupostos estatísticos precisam ser avaliados e portanto algumas análises precisam ser realizadas antes da interpretação do resultado do teste-t. Pressupostos como normalidade (ambos os grupos devem provir de uma população com distribuição normal) e homocedasticidade (A variância entre os dois grupos devem ser iguais). Demonstraremos a frente como realizar alguns desses testes. Mas, primeiro vamos gerar os dados a serem trabalhados para esta etapa. Execute o código abaixo e você irá visualizar no environment do seu RStudio um objeto chamado gastropode que corresponde a um data frame com o conjunto de dados que iremos trabalhar.

OBS: Neste momento não entraremos em detalhes sobre os comandos aplicados para construção dos dados.

grupos <- c(rep(x = "Alimento A", 50), rep(x = "Alimento B", 50))
set.seed(123)
alimento.A <- rnorm(n = 50, mean = 0.7, sd = 0.2)
set.seed(4321)
alimento.B <- rnorm(n = 50, mean = 0.2, sd = 0.2)
Alimento <- c(alimento.A, alimento.B)
gastropode <- as.data.frame(cbind(grupos, round(Alimento, 3)))
colnames(gastropode) <- c("Alimento", "Peso")
rm(list = "grupos", "alimento.A", "alimento.B", "Alimento")

Vamos, agora, verificar os dados por meio da função head() e a estrutura dos dados por meio da função str() e alterar a estrutura dos dados se necessário.

head(gastropode)

##     Alimento  Peso
## 1 Alimento A 0.588
## 2 Alimento A 0.654
## 3 Alimento A 1.012
## 4 Alimento A 0.714
## 5 Alimento A 0.726
## 6 Alimento A 1.043

str(gastropode)

## 'data.frame':    100 obs. of  2 variables:
##  $ Alimento: chr  "Alimento A" "Alimento A" "Alimento A" "Alimento A" ...
##  $ Peso    : chr  "0.588" "0.654" "1.012" "0.714" ...

gastropode$Alimento <- as.factor(gastropode$Alimento)
gastropode$Peso <- as.numeric(gastropode$Peso)
str(gastropode)

## 'data.frame':    100 obs. of  2 variables:
##  $ Alimento: Factor w/ 2 levels "Alimento A","Alimento B": 1 1 1 1 1 1 1 1 1 1 ...
##  $ Peso    : num  0.588 0.654 1.012 0.714 0.726 ...

Agora que importamos e organizamos nossa planilha vamos analisar nosso exemplo.

100 indivíduos de uma espécie de gastropode foi coletada e mantida em cultivo para avaliação da dieta. 50 indivíduos foram mantidos com uma dieta rica no Alimento A e 50 indivíduos com uma dieta rica no Alimento B. Todos os indivíduos foram pesados antes e depois do experimento. A planilha a seguir informa a alteração de peso dos organismos, em gramas, após a dieta oferecida.

Antes de conduzirmos o teste-t vamos praticar fazendo a avaliação gráfica e númerica dos dados.

Os comandos abaixo realizam: o histograma dos dados para Alimento A (Figura 4.6), o histograma dos dados para Alimento B (Figura 4.7) e o boxplot para ambos os dados (Figura 4.8), respectivamente.

Os 2 primeiros gráficos consistem em histogramas em relação aos dados de peso por Alimento. Na primeira linha indicaremos a variável peso dentro da planilha gastropode por meio do operador matemático “$” (cifrão) e selecionamos os dados correspondentes ao Alimento utilizando colchetes [] dentro do qual selecionamos a variável Alimento dentro da planilha gastropode e por meio do sinal de igual duplicado (==) indicamos entre aspas ("“) o grupo (ou categoria) que desejamos. Os demais argumentos já são bem conhecidos e iguais para ambos os histogramas, diferindo apenas o título do gráfico que é definido pelo argumento”main".

hist(gastropode$Peso [gastropode$Alimento == "Alimento A"], 
     xlab = "Alteração do peso", 
     ylab = "Frequência", 
     main = "Alimento A", 
     ylim = c(0, 20),
     xlim = c(-0.5, 1.5))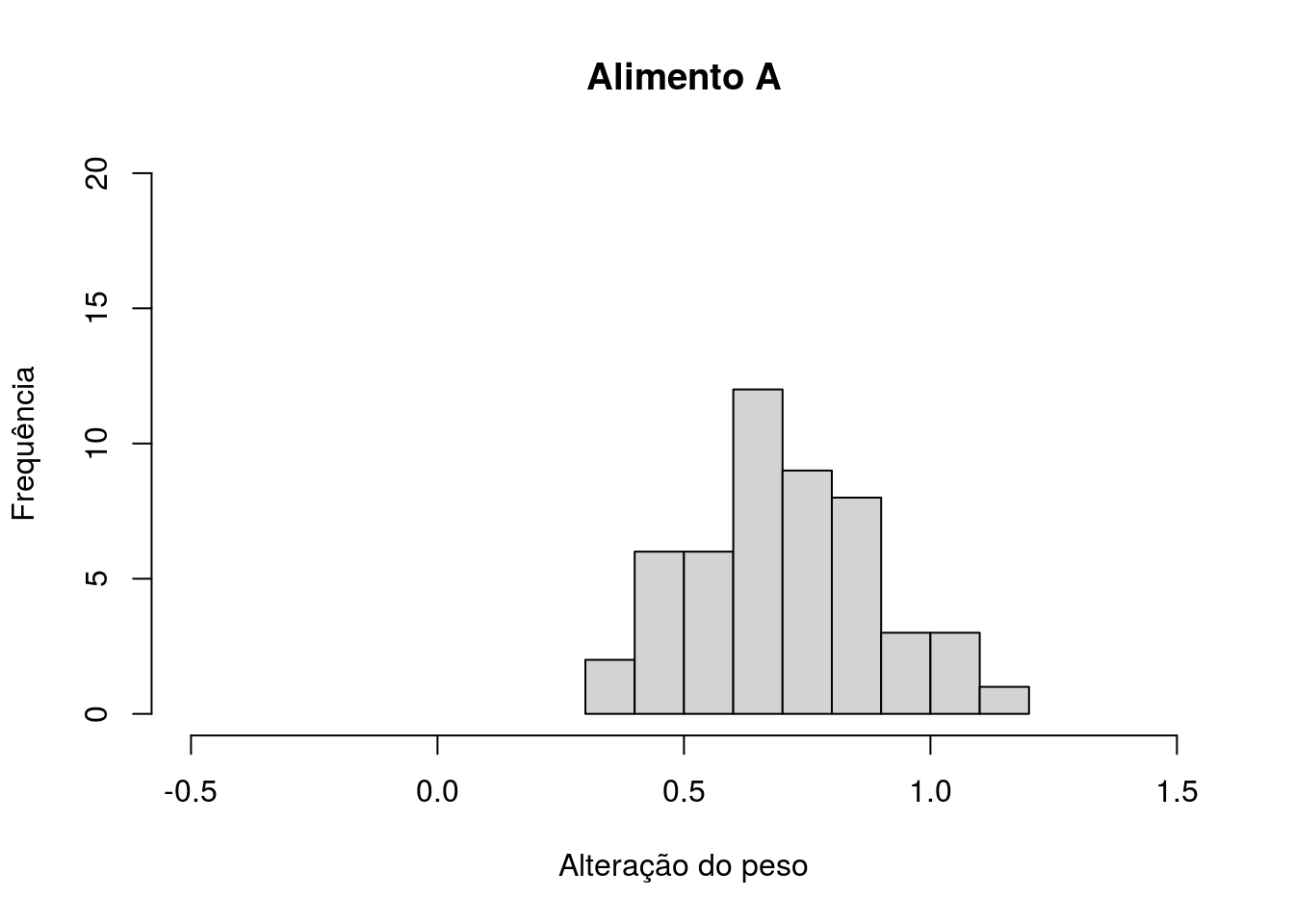

Figura 4.6: Histograma com valores da mudança do peso dos gastrópodes após a dieta com o Alimento A

hist(gastropode$Peso [gastropode$Alimento == "Alimento B"], 
     xlab = "Alteração do peso", 
     ylab = "Frequência", 
     main = "Alimento B",
     ylim = c(0, 20),
     xlim = c(-0.5, 1.5))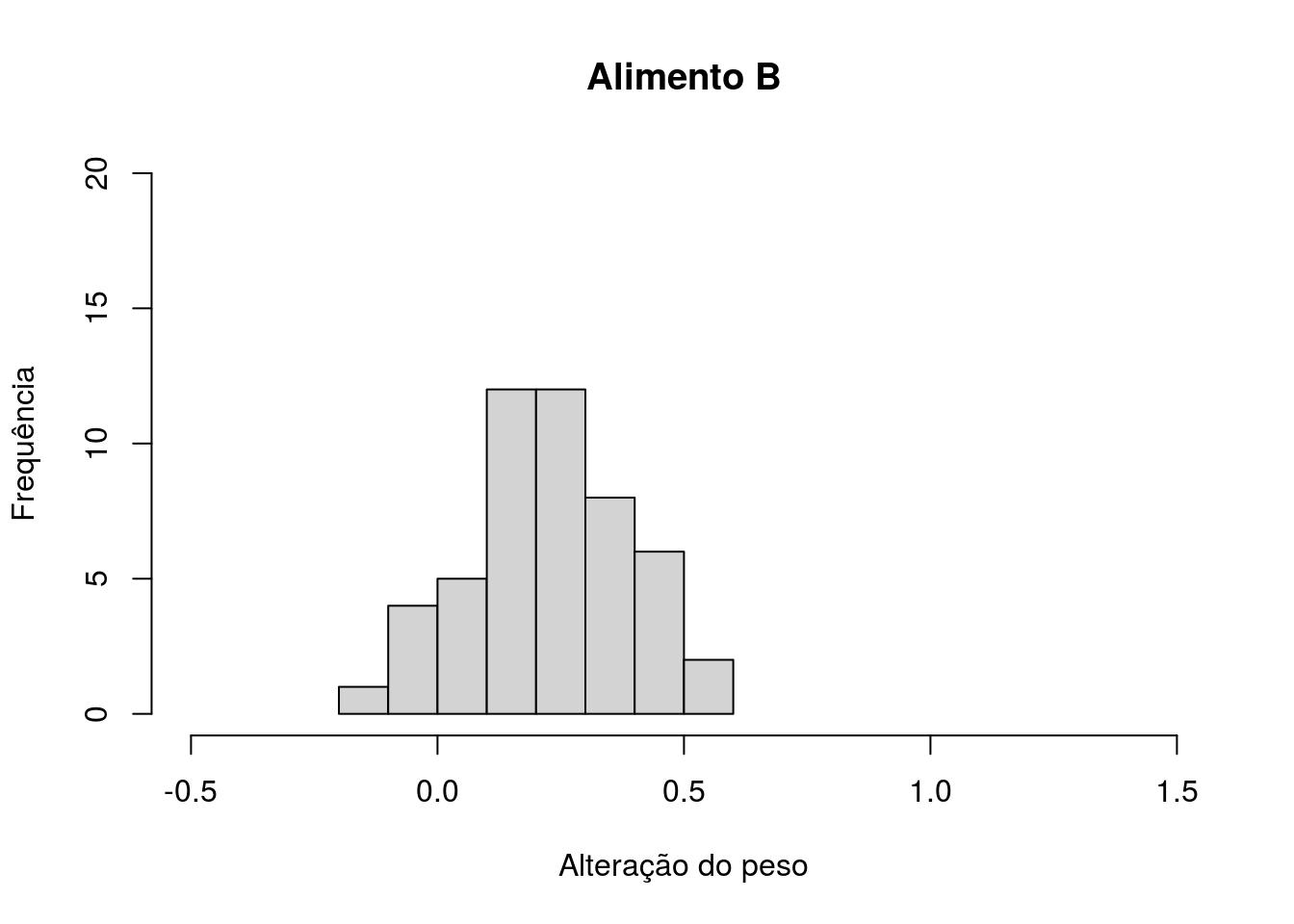

Figura 4.7: Histograma com valores da mudança do peso dos gastrópodes após a dieta com o Alimento B

O Boxplot resume os dados por Alimento e nos indica outras métricas (quartis), como vimos anteriormente no tópico sobre gráficos.

boxplot(Peso ~ Alimento, data = gastropode)

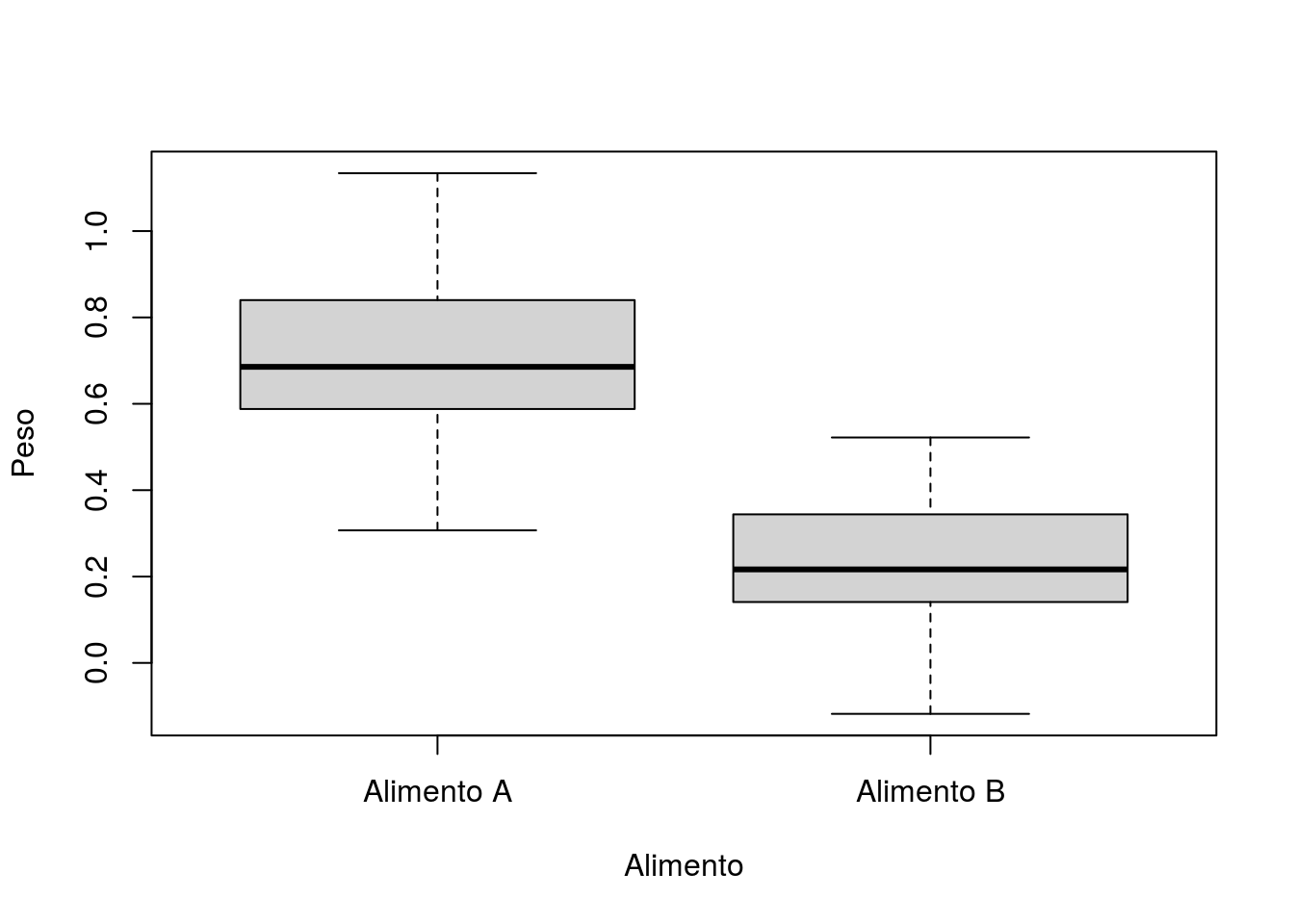
Figura 4.8: Boxplot com os valores da alteração do peso dos gastrópodes por tipo de alimento

Mas se desejarmos observar os valores numéricos que resumem os dados, podemos seguir o que aprendemos anteriormente.

summary(gastropode)

##        Alimento       Peso        
##  Alimento A:50   Min.   :-0.1180  
##  Alimento B:50   1st Qu.: 0.2172  
##                  Median : 0.4475  
##                  Mean   : 0.4652  
##                  3rd Qu.: 0.6843  
##                  Max.   : 1.1340

mean(gastropode$Peso)

## [1] 0.46519

mean(gastropode$Peso [gastropode$Alimento == "Alimento A"])

## [1] 0.7069

mean(gastropode$Peso [gastropode$Alimento == "Alimento B"])

## [1] 0.22348

Utilizando o pacote Rmisc temos uma forma mais simples de escrita e eficiente para observar esses valores e algumas outras métricas.

OBS: Não se esqueça de carregar o pacote por meio da função library().

library(Rmisc)
summarySE(data = gastropode, measurevar = "Peso", groupvars = "Alimento")

##     Alimento  N    Peso        sd         se         ci
## 1 Alimento A 50 0.70690 0.1852070 0.02619223 0.05263525
## 2 Alimento B 50 0.22348 0.1573551 0.02225337 0.04471982

Até o momento observamos como estão os nossos dados e podemos ver que a administração do “Alimento A” resultou em um maior ganho de peso pelos gastropodes do que a “Alimento B”. Mas será que o que observamos grafica e numericamente se reflete estatisticamente? Vamos a nossa avaliação dos pressupostos do teste-t para duas amostras e se cumpridos vamos para o teste-t.

Uma das formas mais convencionais de avaliar a normalidade é pelo teste de Shapiro-Wilks aplicando a função shapiro.test() e a homocedasticidade pelo teste de Bartlett bartlett.test(). Para o teste de normalidade de Shapiro-Wilks devemos aplica-lo à variável númerica desejada (ex: Peso) e realiza-lo para cada categória (ex: “Alimento A” e “Alimento B”) da variável categorica escolhida (ex: Alimento) separadamente. Para o teste de homocedasticidade de Bartlett devemos avaliar a variável mensurável (ex: Peso) em função da variável categorica (ex: Alimento). Veja os comandos e resultado abaixo.

shapiro.test(gastropode$Peso [gastropode$Alimento == "Alimento A"])

## 
##  Shapiro-Wilk normality test
## 
## data:  gastropode$Peso[gastropode$Alimento == "Alimento A"]
## W = 0.98923, p-value = 0.9266

shapiro.test(gastropode$Peso [gastropode$Alimento == "Alimento B"])

## 
##  Shapiro-Wilk normality test
## 
## data:  gastropode$Peso[gastropode$Alimento == "Alimento B"]
## W = 0.98059, p-value = 0.5769

bartlett.test(Peso ~ Alimento, data = gastropode)

## 
##  Bartlett test of homogeneity of variances
## 
## data:  Peso by Alimento
## Bartlett's K-squared = 1.2826, df = 1, p-value = 0.2574

Como podemos observar, ambos os grupos apresentam dados normais e homocedásticos, para um nível de confiança de 95%, já que o p-value foi superior a 0,05. Dessa forma vamos dar continuidade a nossa análise e verificar se as médias dos grupos são diferentes aplicando a já conhecida função t.test().

t.test(Peso ~ Alimento, 
       data = gastropode,
       var.equal = TRUE,
       conf.level = 0.95)

## 
##  Two Sample t-test
## 
## data:  Peso by Alimento
## t = 14.065, df = 98, p-value < 2.2e-16
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  0.4152153 0.5516247
## sample estimates:
## mean in group Alimento A mean in group Alimento B 
##                  0.70690                  0.22348

Repare que a forma da escrita se alterou um pouco. Mas como podem ver, nada complicado. Agora escrevemos a variável mensurável (Peso) em função da (~) variável categórica (Alimento). Guarde bem essa forma de escrita (similar ao que realizamos no boxplot e barplot) pois ela será utilizada para praticamente todos os testes a partir daqui e para inúmeras outras funções. Adcionamos o argumento “data” que indica a planilha de onde estamos utilizando as variáveis, o argumento “var.equal” o qual indica que a variância entre os grupos é igual¹⁷ e o argumento “conf.level” o qual define o nível de confiança com qual estamos trabalhando.

De acordo com nosso resultado podemos ver que o valor do teste-t é 14,065, o grau de liberdade de 98 (o qual consiste no total de observações subtraído de um por grupo), o valor de probabilidade associado ao teste (p-value = \(2,2\times10^{-16}\)), o intervalo de confiança de 95% (0,415 e 0,551) que refere-se a diferença da média entre os grupos (a diferença da média dos grupos é: 0,70690 - 0,22348 = 0,48342), ou seja, o intervalo de confiança é em função dessa diferença e as últimas linhas do resultado representam as médias de alteração do peso para cada Alimento (Alimento A = 0,70690 e Alimento B = 0,22348). De acordo com esse resultado refutamos a hipótese nula de que as médias são similares. Portanto podemos dizer que dependendo do Alimento (A ou B) utilizada na dieta podemos ter diferentes alterações no peso dos gastropodes.

Da mesma forma que avaliamos para o teste-t de uma amostra, podemos plotar o resultado como um gráfico da função de densidade do teste-t. Só devemos lembrar de carregar o pacote webr.

library(webr)
plot(t.test(Peso ~ Alimento, 
            data = gastropode,
            var.equal = TRUE,
            conf.level = 0.95))

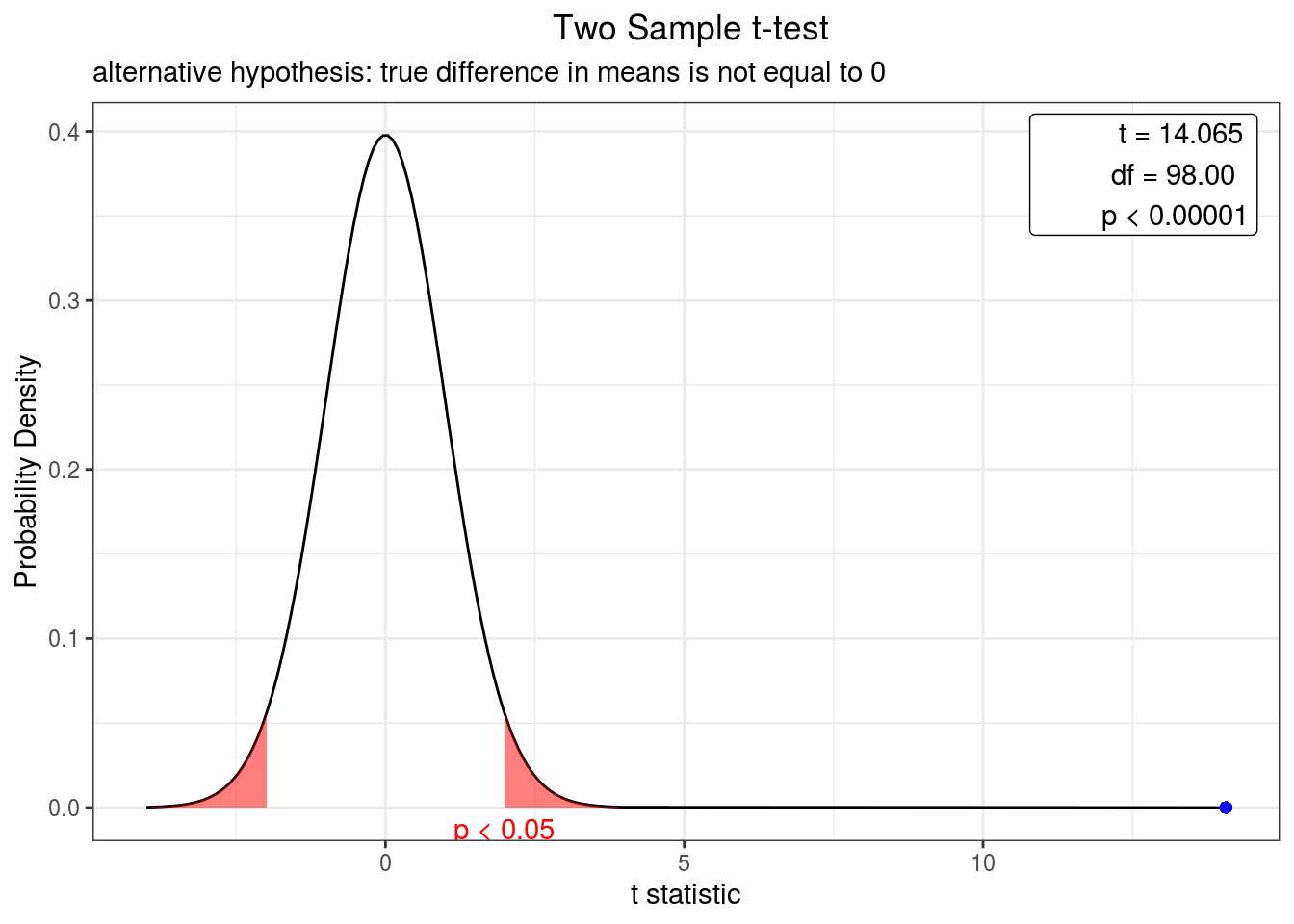
Figura 4.9: Curva de densidade representando o valor do teste-t bicaudal para a alteração do peso de gastrópodes em relação ao alimento a um intervalo de confiança de 95%. O ponto azul indica o valor do teste.

Neste gráfico podemos ver que o resultado do teste-t (Figura 4.9), indicado pelo ponto azul, está muito além do nível da zona de rejeição, indicando que os dois grupos apresentam médias bem diferentes, ou seja, a diferença entre as duas médias é altamente significativa.

Vamos exercitar nosso conhecimento em R e teste-t com um outro exemplo (Gere os dados abaixo).

OBS: Neste momento não entraremos em detalhes sobre os comandos aplicados para construção dos dados.

grupos <- c(rep(x = "Ano 0", 36), rep(x = "Ano 20", 36))
set.seed(245)
ano.0 <- rnorm(n = 36, mean = 15.7, sd = 0.2) + runif(n = 36)
set.seed(356)
ano.20 <- rnorm(n = 36, mean = 16.2, sd = 0.5) + runif(n = 36)
ano <- c(ano.0, ano.20)
lagoa <- as.data.frame(cbind(grupos, round(ano, 3)))
colnames(lagoa) <- c("Ano", "Temperatura")
rm(list = "grupos", "ano.0", "ano.20", "ano")

Imagine que durante um ano você mensurou a temperatura de uma lagoa três vezes por mês durante todos os meses ao longo de um ano. 20 anos depois você retornou a lagoa e mensurou novamente a temperatura três vezes por mês durante um ano. Considerando um nível de confiança de 99% a temperatura é igual ou diferente entre os anos?

A primeira coisa que devemos fazer é escrever nossa hipótese. Vamos a ela.

• H0: A média da temperatura é igual entre os anos (\(\mu_{ano0} = \mu_{ano 20}\));
• HA: A média da temperatura é diferente entre os anos (\(\mu_{ano0} \neq \mu_{ano 20}\));

Com a hipótese construída vamos verificar a estrutura dos dados (modificar se necessário) e sumarizar nossos dados grafica e estatisticamente. Conforme realizado no exemplo anterior.

Os comandos abaixo realizam a análise gráfica: o histograma dos valores de temperatura no “ano 0” (Figura 4.10), o histograma dos valores de temperatura no “ano 20” (Figura 4.11) e o boxplot para ambos os dados (Figura 4.12), respectivamente. Quanto ao seu resultado podemos notar uma maior temperatura média anual da lagoa 20 anos depois da primeira amostragem.

head(lagoa)

##     Ano Temperatura
## 1 Ano 0      16.345
## 2 Ano 0      16.383
## 3 Ano 0      15.727
## 4 Ano 0      16.058
## 5 Ano 0      15.842
## 6 Ano 0      16.158

str(lagoa)

## 'data.frame':    72 obs. of  2 variables:
##  $ Ano        : chr  "Ano 0" "Ano 0" "Ano 0" "Ano 0" ...
##  $ Temperatura: chr  "16.345" "16.383" "15.727" "16.058" ...

lagoa$Ano <- as.factor(lagoa$Ano)
lagoa$Temperatura <- as.numeric(lagoa$Temperatura)
str(lagoa)

## 'data.frame':    72 obs. of  2 variables:
##  $ Ano        : Factor w/ 2 levels "Ano 0","Ano 20": 1 1 1 1 1 1 1 1 1 1 ...
##  $ Temperatura: num  16.3 16.4 15.7 16.1 15.8 ...

hist(lagoa$Temperatura [lagoa$Ano == "Ano 0"], 
     xlab = "Temperatura (°C)", 
     ylab = "Frequência", 
     main = "Ano 0", 
     ylim = c(0, 15),
     xlim = c(15, 19))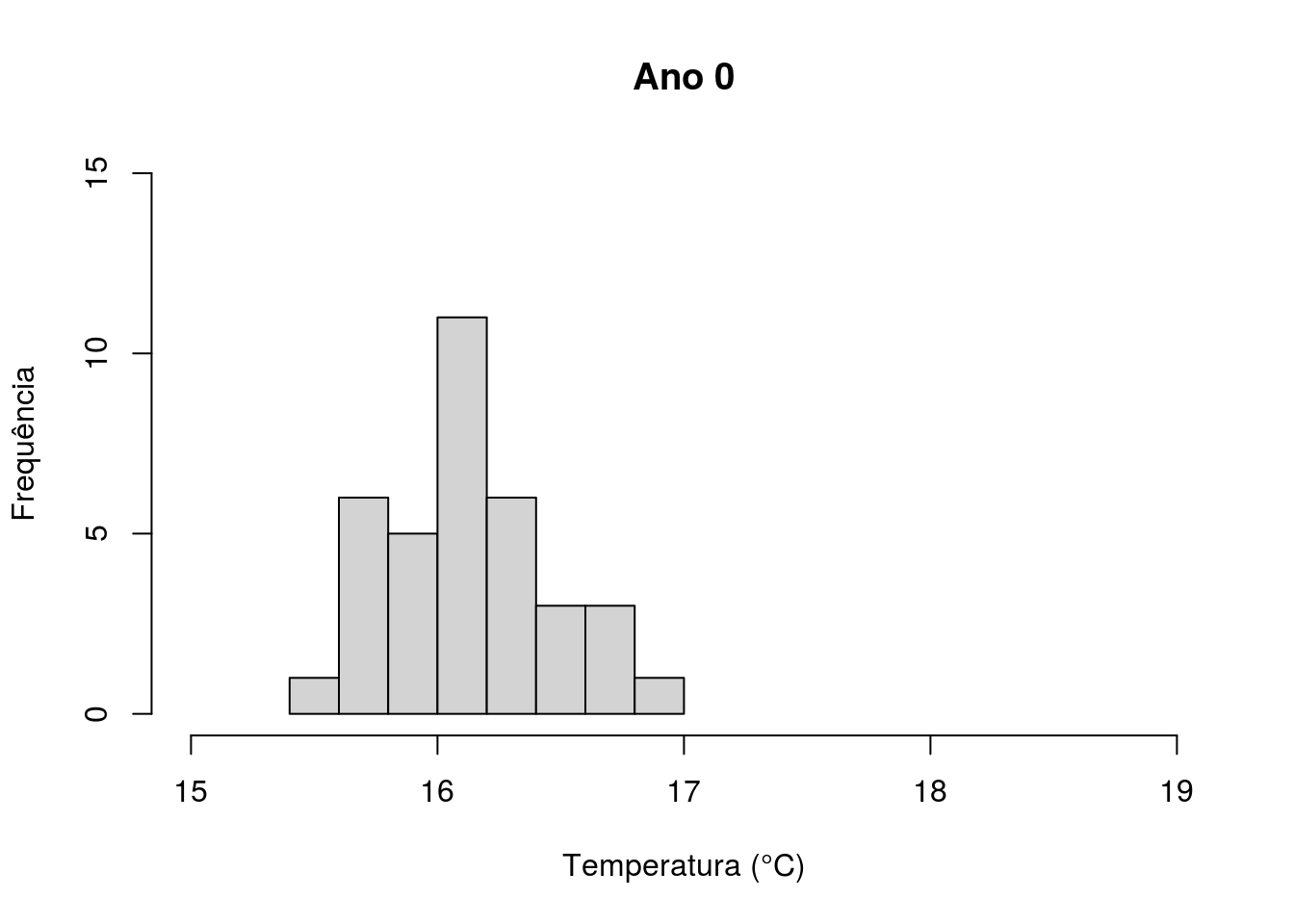

Figura 4.10: Histograma com valores de temperatura da lagoa no Ano 0.

hist(lagoa$Temperatura [lagoa$Ano == "Ano 20"], 
     xlab = "Temperatura (°C)", 
     ylab = "Frequência", 
     main = "Ano 20", 
     ylim = c(0, 15),
     xlim = c(15, 19))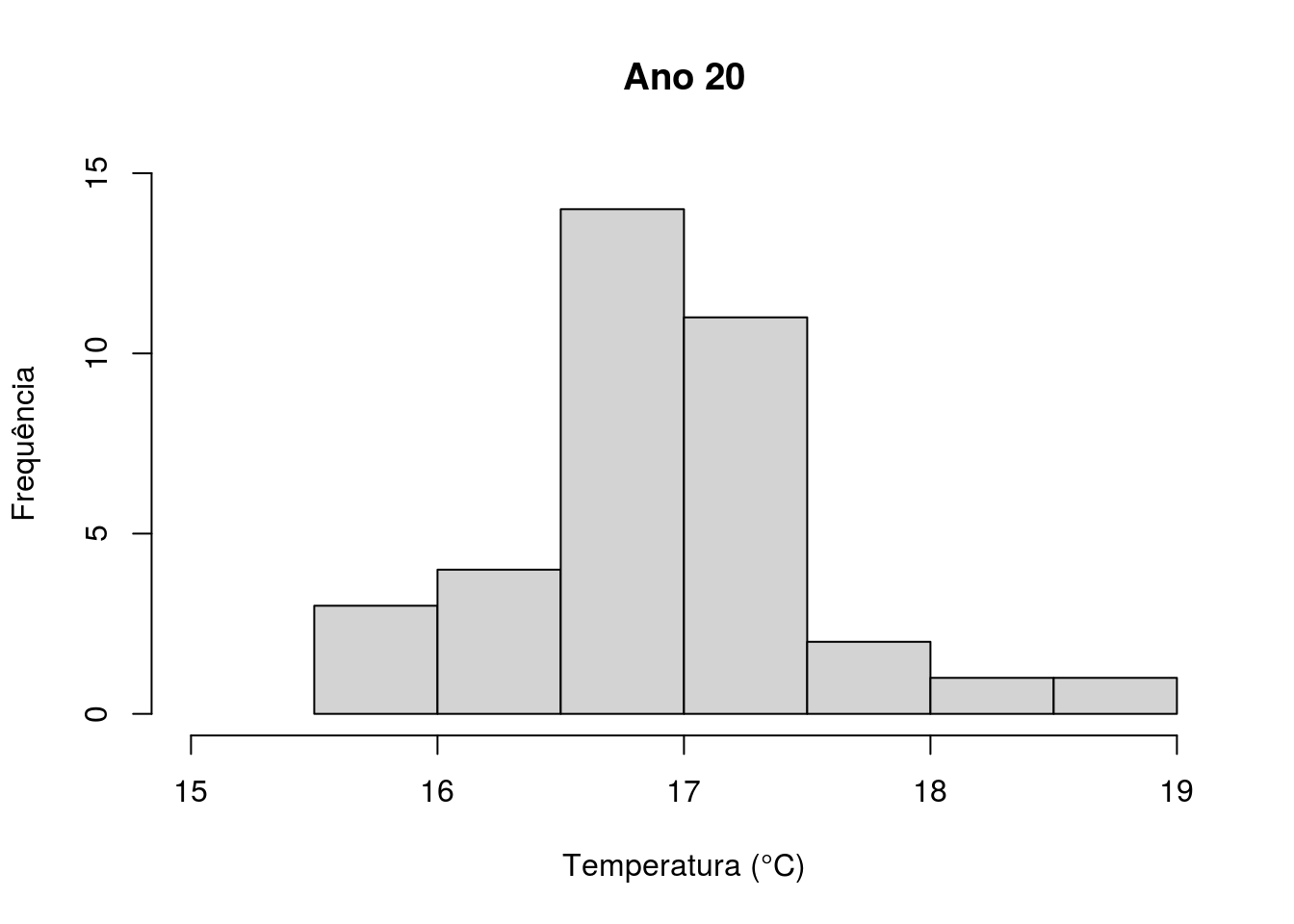

Figura 4.11: Histograma com valores de temperatura da lagoa no Ano 20.

boxplot(Temperatura ~ Ano, data = lagoa)

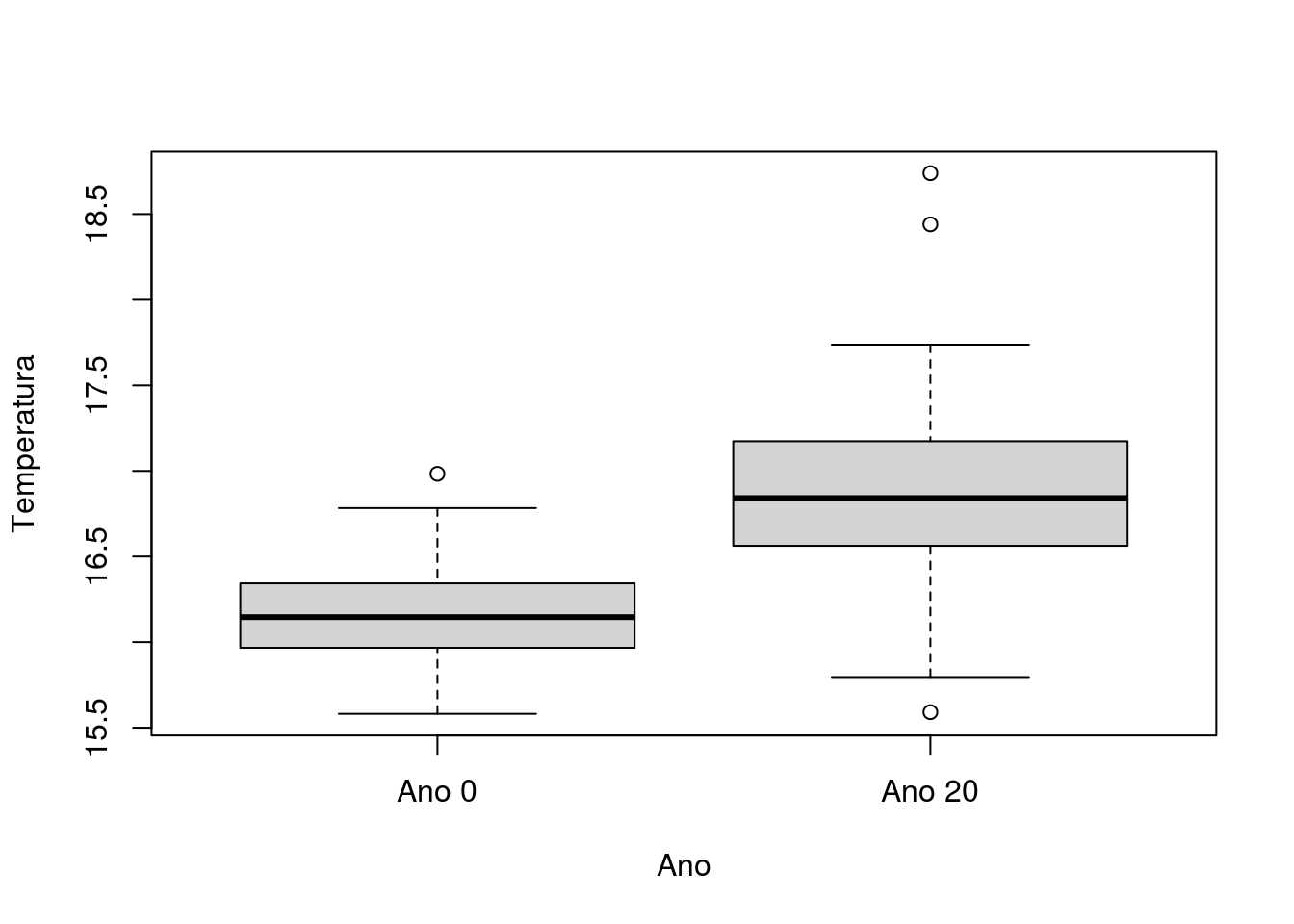
Figura 4.12: Boxplot com os valores de temperatura da lagoa por ano.

Abaixo temos o comando para realizar a sumarização numérica dos dados.

summary(lagoa)

##      Ano      Temperatura   
##  Ano 0 :36   Min.   :15.58  
##  Ano 20:36   1st Qu.:16.08  
##              Median :16.41  
##              Mean   :16.52  
##              3rd Qu.:16.86  
##              Max.   :18.74

library(Rmisc)
summarySE(data = lagoa, measurevar = "Temperatura", groupvars = "Ano")

##      Ano  N Temperatura        sd         se        ci
## 1  Ano 0 36    16.14661 0.3301591 0.05502652 0.1117098
## 2 Ano 20 36    16.89750 0.6409853 0.10683089 0.2168782

Aplicando a função summarySE() do pacote Rmisc sumarizamos nossos dados como mostrado acima e em relação aos valores de média e desvios podemos observar que a média é bem próxima, mas será que elas são estatisticamente iguais? Para isso vamos realizar o teste-t.

Antes do teste-t vamos calcular os pressupostos requeridos, normalidade e homocedasticidade. Conforme realizado no exemplo anterior.

shapiro.test(lagoa$Temperatura [lagoa$Ano == "Ano 0"])

## 
##  Shapiro-Wilk normality test
## 
## data:  lagoa$Temperatura[lagoa$Ano == "Ano 0"]
## W = 0.97181, p-value = 0.4771

shapiro.test(lagoa$Temperatura [lagoa$Ano == "Ano 20"])

## 
##  Shapiro-Wilk normality test
## 
## data:  lagoa$Temperatura[lagoa$Ano == "Ano 20"]
## W = 0.9571, p-value = 0.1747

bartlett.test(Temperatura ~ Ano, data = lagoa)

## 
##  Bartlett test of homogeneity of variances
## 
## data:  Temperatura by Ano
## Bartlett's K-squared = 14.189, df = 1, p-value = 0.0001653

Como podemos ver os dados são normais, porém não são homocedasticos (a variância não é igual entre os grupos). Neste caso podemos fazer um teste-t de Welch (este teste aplica uma correção quando as variâncias não são iguais). Contudo, o teste de Welch ele é comumente usado quando o N amostral é considerado baixo (menor que 10 para um dos dois grupos). Vamos Analisar o teste-t considerando a variância igual e desigual para ver se há diferença significativa no resultado do teste ou não.

t.test(Temperatura ~ Ano, 
       data = lagoa,
       var.equal = TRUE,
       conf.level = 0.99)

## 
##  Two Sample t-test
## 
## data:  Temperatura by Ano
## t = -6.2486, df = 70, p-value = 2.837e-08
## alternative hypothesis: true difference in means is not equal to 0
## 99 percent confidence interval:
##  -1.069087 -0.432691
## sample estimates:
##  mean in group Ano 0 mean in group Ano 20 
##             16.14661             16.89750

t.test(Temperatura ~ Ano, 
       data = lagoa,
       var.equal = FALSE,
       conf.level = 0.99)

## 
##  Welch Two Sample t-test
## 
## data:  Temperatura by Ano
## t = -6.2486, df = 52.35, p-value = 7.594e-08
## alternative hypothesis: true difference in means is not equal to 0
## 99 percent confidence interval:
##  -1.0721092 -0.4296686
## sample estimates:
##  mean in group Ano 0 mean in group Ano 20 
##             16.14661             16.89750

Como podem notar a forma de escrever o teste é similar ao exemplo anterior as alterações consistem nas variáveis e no conjunto de dados utilizado e como foi pedido no teste a alteração do nível de confiança para 99% (conf.level = 0,99) e os dois teste-t (com variância igual e com variância desigual - Welch).

Olhando para os dois resultados ambos os testes demonstraram diferenças significativas entre os anos, pois o p-value foi menor que 0,01 (lembrar que como o nível de confiança foi alterado para 0,99 a significância só ocorrerá se o p-value for menor que 0,01, como é o caso). Porém podemos ver que não há muita diferença em relação aos valores de ambos os testes-t, pois como ressaltamos a aplicação do teste de Welch apresenta maior peso quando as variâncias são desiguais e o número amostral de um dos grupos é muito pequeno (<10).

Assim como fizemos anteriormente vamos olhar o resultado em relação a distribuição da função de densidade do teste-t para um nível de confiança de 99% (Figura 4.13). Só devemos lembrar de carregar o pacote webr, se ainda não foi carregado.

library(webr)
plot(t.test(Temperatura ~ Ano, 
            data = lagoa,
            var.equal = TRUE,
            conf.level = 0.99))

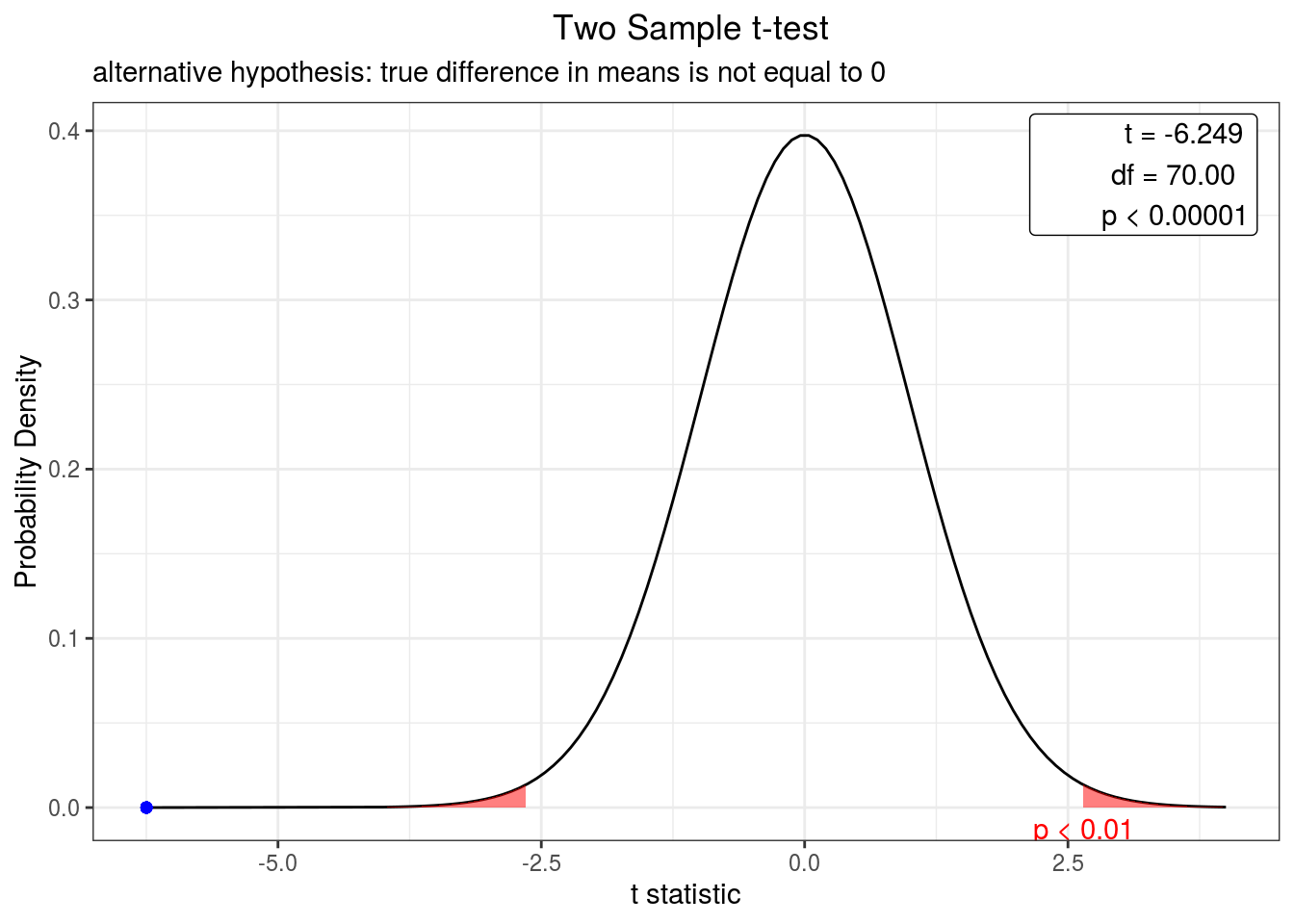
Figura 4.13: Curva de densidade representando o valor do teste-t bicaudal para comparação da temperatura em um lago entre dois anos a um intervalo de confiança de 99%. O ponto azul indica o valor do teste.

De acordo com esse exemplo podemos afirmar que os anos diferem entre si e que em 20 anos a lagoa amostrada apresentou um aumento da temperatura.

4.3 Teste-t pareado

Aplicamos este teste quando as duas amostras de uma variável categórica são independentes e desejamos verificar se os pares de observações entre os grupos diferem entre si (Tabela 4.3). Cada observação de ambas as amostras devem estar associadas para podermos dizer que ocorrem em pares.

Tabela 4.3: Principais características do teste-t pareado

Atributos	Características
Tipo de variável	Quantitativa e categórica
Quantidade de variáveis	3 (1 quantitativa e 2 categóricas)
Hipótese nula	A diferença na média da variável quantitativa entre os pares de grupos é igual a 0.
Fórmula	\[t=\frac{\overline{d}}{s_{\overline{d}}}\], onde, \(\overline{d}\): média da diferença entre os pares de observações entre os grupos, \(s_{\overline{d}}\): erro padrão da diferença entre os pares de observações entre os grupos.
Observação	Não há a necessidade de post-hoc nem expressa-la graficamente.

Vejamos um exemplo de como conduzir essa análise.

Imagine que dois pesquisadores embarcaram com objetivo de fazer contagem de aves em alto mar. Após 20 dias de observações, independentes entre os observadores, obtivemos os dados abaixo.

Começaremos gerando os dados e o modificando conforme o necessário.

OBS: Neste momento não entraremos em detalhes sobre os comandos aplicados para construção dos dados.

set.seed(2328)
aves.1 <- rnorm(n = 20, mean = 20, sd = 1) + runif(n = 20)
set.seed(3230)
aves.2 <- rnorm(n = 20, mean = 21, sd = 2) + runif(n = 20)
dia <- c("Dia 1", "Dia 2", "Dia 3", "Dia 4", "Dia 5", "Dia 6", "Dia 7", "Dia 8", 
         "Dia 9", "Dia 10", "Dia 11", "Dia 12", "Dia 13", "Dia 14", "Dia 15", "Dia 16",
         "Dia 17", "Dia 18", "Dia 19", "Dia 20")
aves <- as.data.frame(cbind(dia, round(aves.1, 0), round(aves.2, 0)))
colnames(aves) <- c("Dia", "Observador.1", "Observador.2")
rm(list = "aves.1", "aves.2", "dia")

Nestes casos temos as seguintes hipoteses:

• H0: A diferença na média do número de observações de aves entre os Observadores é igual a 0.
• HA: A diferença na média do número de observações de aves entre os Observadores difere de 0.

Vamos verificar a estrutura dos dados e modificar conforme a necessidade.

head(aves)

##     Dia Observador.1 Observador.2
## 1 Dia 1           19           20
## 2 Dia 2           20           22
## 3 Dia 3           18           23
## 4 Dia 4           22           18
## 5 Dia 5           22           22
## 6 Dia 6           22           23

str(aves)

## 'data.frame':    20 obs. of  3 variables:
##  $ Dia         : chr  "Dia 1" "Dia 2" "Dia 3" "Dia 4" ...
##  $ Observador.1: chr  "19" "20" "18" "22" ...
##  $ Observador.2: chr  "20" "22" "23" "18" ...

aves$Dia <- as.factor(aves$Dia)
aves$Observador.1 <- as.numeric(aves$Observador.1)
aves$Observador.2 <- as.numeric(aves$Observador.2)
str(aves)

## 'data.frame':    20 obs. of  3 variables:
##  $ Dia         : Factor w/ 20 levels "Dia 1","Dia 10",..: 1 12 14 15 16 17 18 19 20 2 ...
##  $ Observador.1: num  19 20 18 22 22 22 21 20 22 21 ...
##  $ Observador.2: num  20 22 23 18 22 23 20 24 22 24 ...

Neste exemplo podemos perceber que temos as variáveis categóricas “Dia” e observadores os quais estão em colunas como: “Observador 1” e “Observador 2” e a variável quantitativa “aves” que consiste no número de aves avistadas.

Vamos sumarizar os dados grafica e estatisticamente.

Primeiro vejamos nossos histogramas relativos a observações em relação aos observadores (Figura 4.14 e 4.15).

hist(aves$Observador.1, 
     xlab = "Observações", 
     ylab = "Frequência", 
     main = "Observador 1", 
     ylim = c(0, 10),
     xlim = c(18, 25))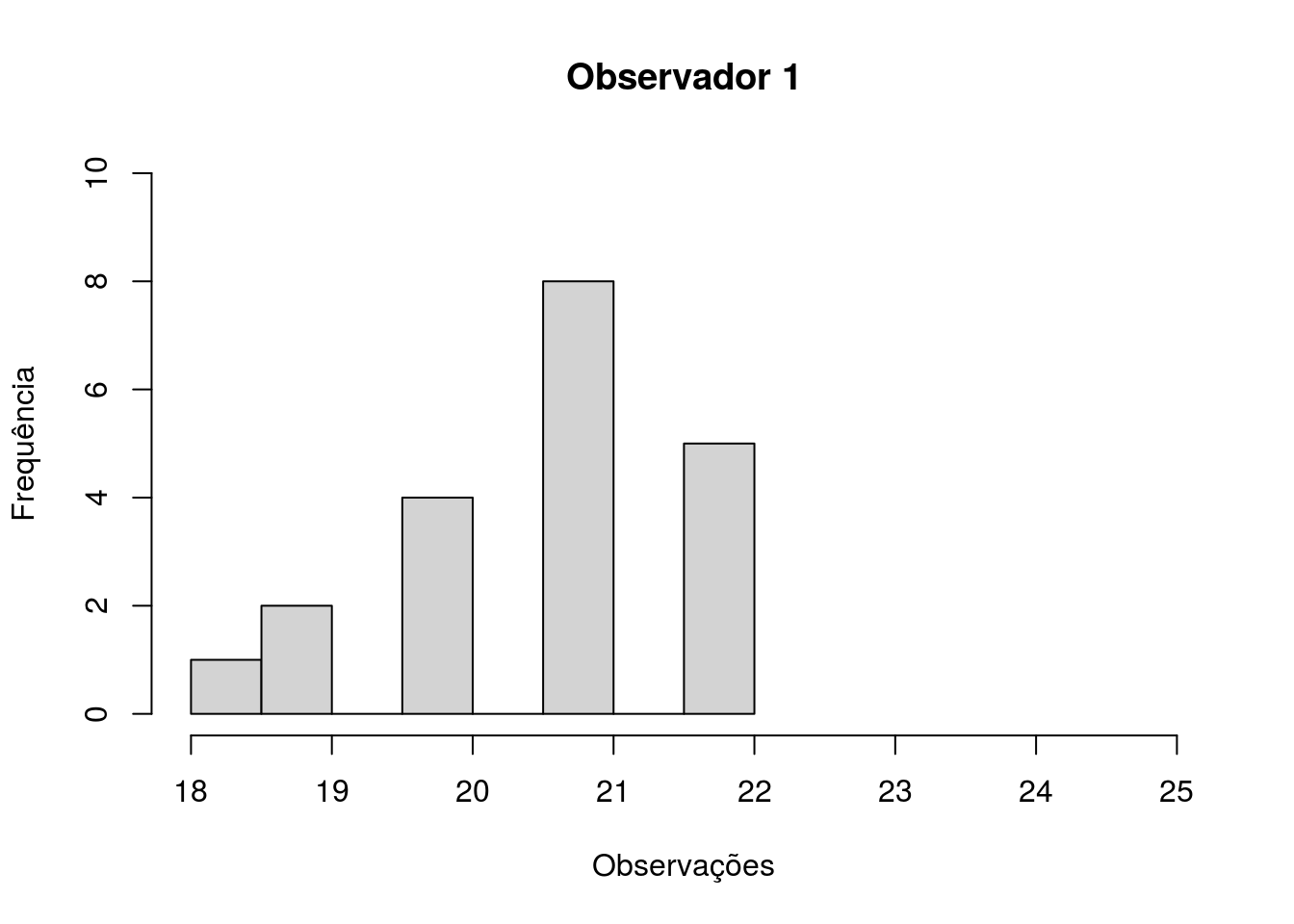

Figura 4.14: Histograma com a frequência de observações de aves, por 20 dias, pelo observador 1

hist(aves$Observador.2, 
     xlab = "Observações", 
     ylab = "Frequência", 
     main = "Observador 2", 
     ylim = c(0, 10),
     xlim = c(18, 25))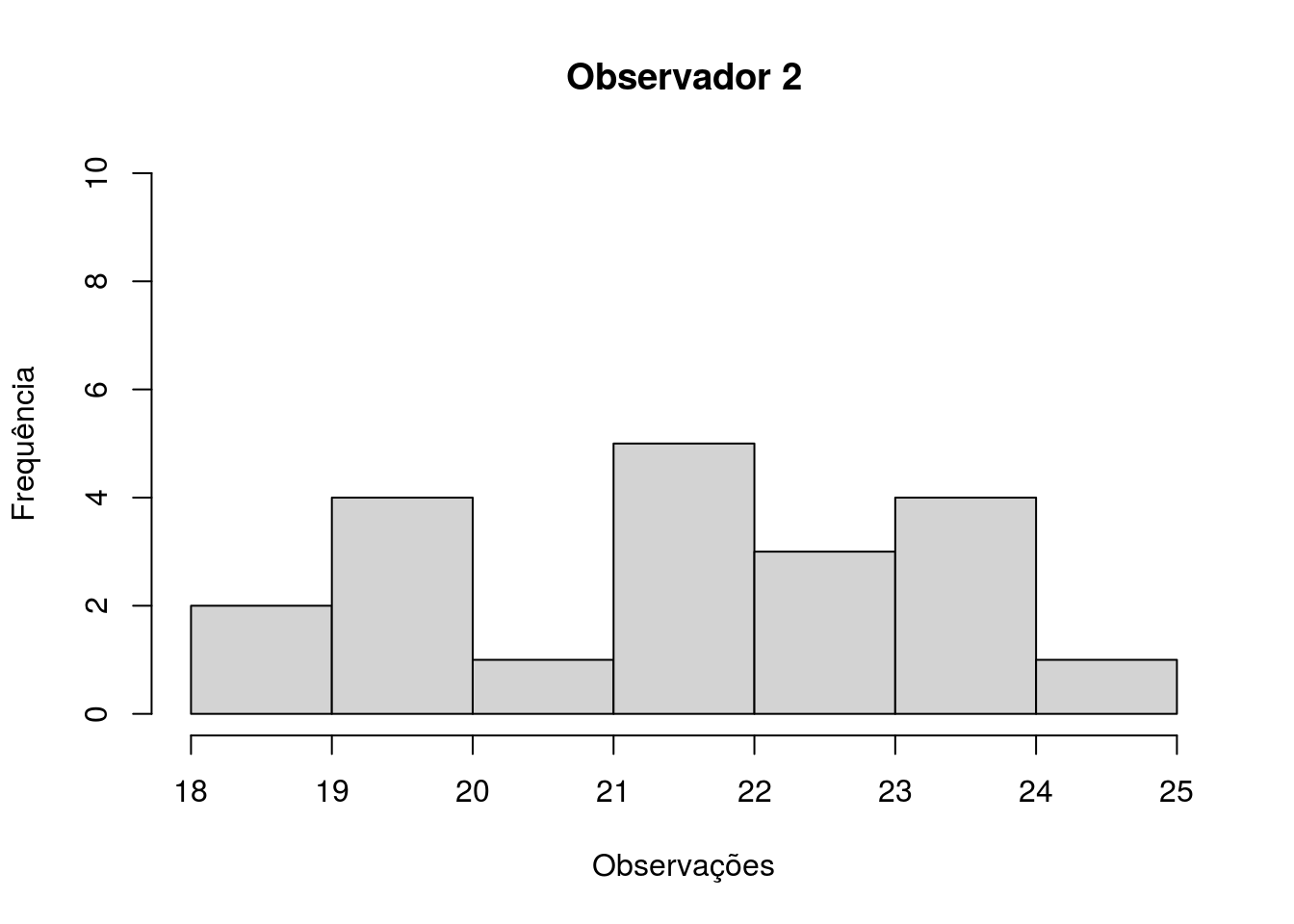

Figura 4.15: Histograma com a frequência de observações de aves, por 20 dias, pelo observador 2

Agora vejamos o boxplot, repare que neste caso a sua escrita difere um pouco do que fizemos nos exemplos anteriores, pois agora inserimos a coluna referente ao “Observador 1” e depois a coluna referente ao “Observador 2” ((Figura 4.16). Isso se deve ao fato da planilha estar estruturada de forma diferente das anteriores. Não utilizamos o til (~), mas inserimos o nome da planilha seguido pelo operador matemático “$” (cifrão) mais o nome da variável quantitativa que queremos representar. Inserimos também outros 2 argumentos que são “names” com dois nomes concatenados pela função c() que representam as variaveis quantitativas na ordem em que foram inseridas e o argumento “ylab” que dá nome ao eixo y.

boxplot(aves$Observador.1, 
        aves$Observador.2, 
        names = c("Observador 1", "Observador 2"),
        ylab = "Frequência de Observações")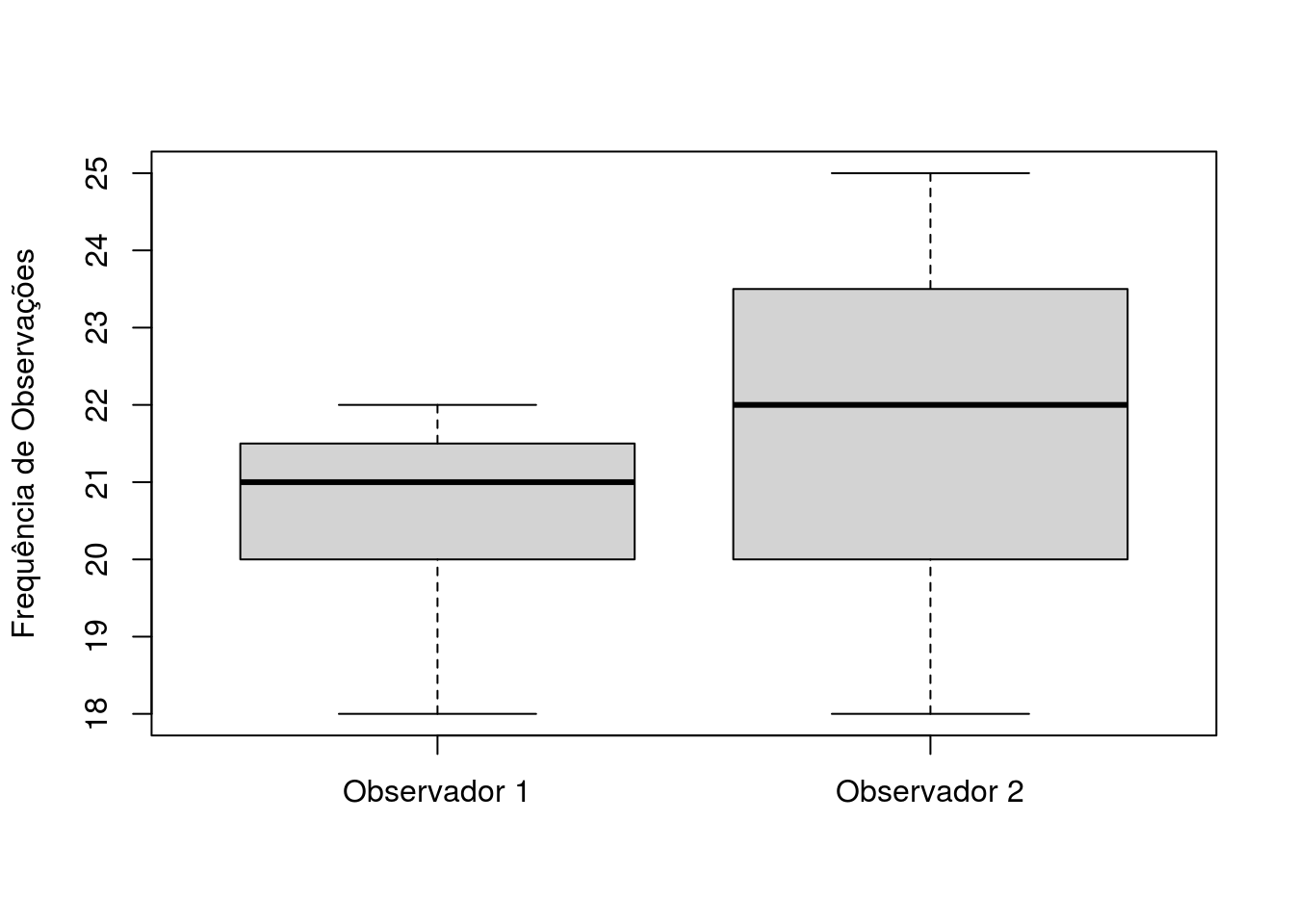

Figura 4.16: Boxplot com as frequências de observações de aves por 20 dias de 2 observadores.

Vejamos o o resumo de nossos dados utilizando a função padrão do R summary.

summary(aves)

##       Dia      Observador.1    Observador.2  
##  Dia 1  : 1   Min.   :18.00   Min.   :18.00  
##  Dia 10 : 1   1st Qu.:20.00   1st Qu.:20.00  
##  Dia 11 : 1   Median :21.00   Median :22.00  
##  Dia 12 : 1   Mean   :20.70   Mean   :21.90  
##  Dia 13 : 1   3rd Qu.:21.25   3rd Qu.:23.25  
##  Dia 14 : 1   Max.   :22.00   Max.   :25.00  
##  (Other):14

Como podemos notar, devido a organização dos dados na planilha a função summary() já resume de maneira adequada nossos dados.

Em relação ao resumo dos nossos dados temos que o observador 2 contabilizou um número maior de aves que o observador 1, mas será que a diferença nos pares de observações é zero? De outra maneira, será que a média da diferença entre os pares de obsevações de aves entre os observadores é similar?

O teste-t pareado não apresenta pressuposto quanto aos dados, porém como ele avalia a diferença entre dois grupos o pressuposto requerido é a normalidade da diferença dos dados. Vamos a nossa avaliação do pressuposto.

Primeiro vamos criar um objeto que consiste na diferença entre observadores

diferenca <- aves$Observador.1 - aves$Observador.2

Agora vamos realizar o teste de normalidade da diferença.

shapiro.test(diferenca)

## 
##  Shapiro-Wilk normality test
## 
## data:  diferenca
## W = 0.98173, p-value = 0.9544

De acordo com o teste de Shapiro os dados são normais. Vamos a nossa avaliação pelo teste-t.

t.test(aves$Observador.1,
       aves$Observador.2,
       paired = TRUE,
       conf.level = 0.95)

## 
##  Paired t-test
## 
## data:  aves$Observador.1 and aves$Observador.2
## t = -2.1608, df = 19, p-value = 0.04369
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -2.36237491 -0.03762509
## sample estimates:
## mean of the differences 
##                    -1.2

Para a execução do teste-t pareado 2 diferenças podem ser notadas na escrita da função, em relação ao teste-t para duas amostras. A primeira consiste no fato de que não utilizamos o til (~), mas sim as variáveis referentes as observações e a segunda é o argumento “paired” que tem valor lógico (ou seja, TRUE ou FALSE) e indicamos ele como “TRUE” (verdadeiro).

Quanto ao resultado podemos notar que nos é informado que o teste consiste num teste-t pareado e que o número de aves observadas pelos observadores é ligeiramente diferente a um nível de confiança de 95%, visto que o p-value é próximo à 0,05 e na última linha nos é indicado que a média da diferença das observações é de -1,2. Em outras palavras o teste nos diz que a média das diferenças nas observações de aves é diferente de 0¹⁸, portanto rejeitamos a hipótese nula.

Assim como fizemos anteriormente vamos olhar o resultado em relação a distribuição função de densidade do teste-t (Figura 4.17). Só devemos lembrar de carregar o pacote webr se ainda não foi carregado.

library(webr)
plot(t.test(aves$Observador.1,
            aves$Observador.2,
            paired = TRUE,
            conf.level = 0.95))

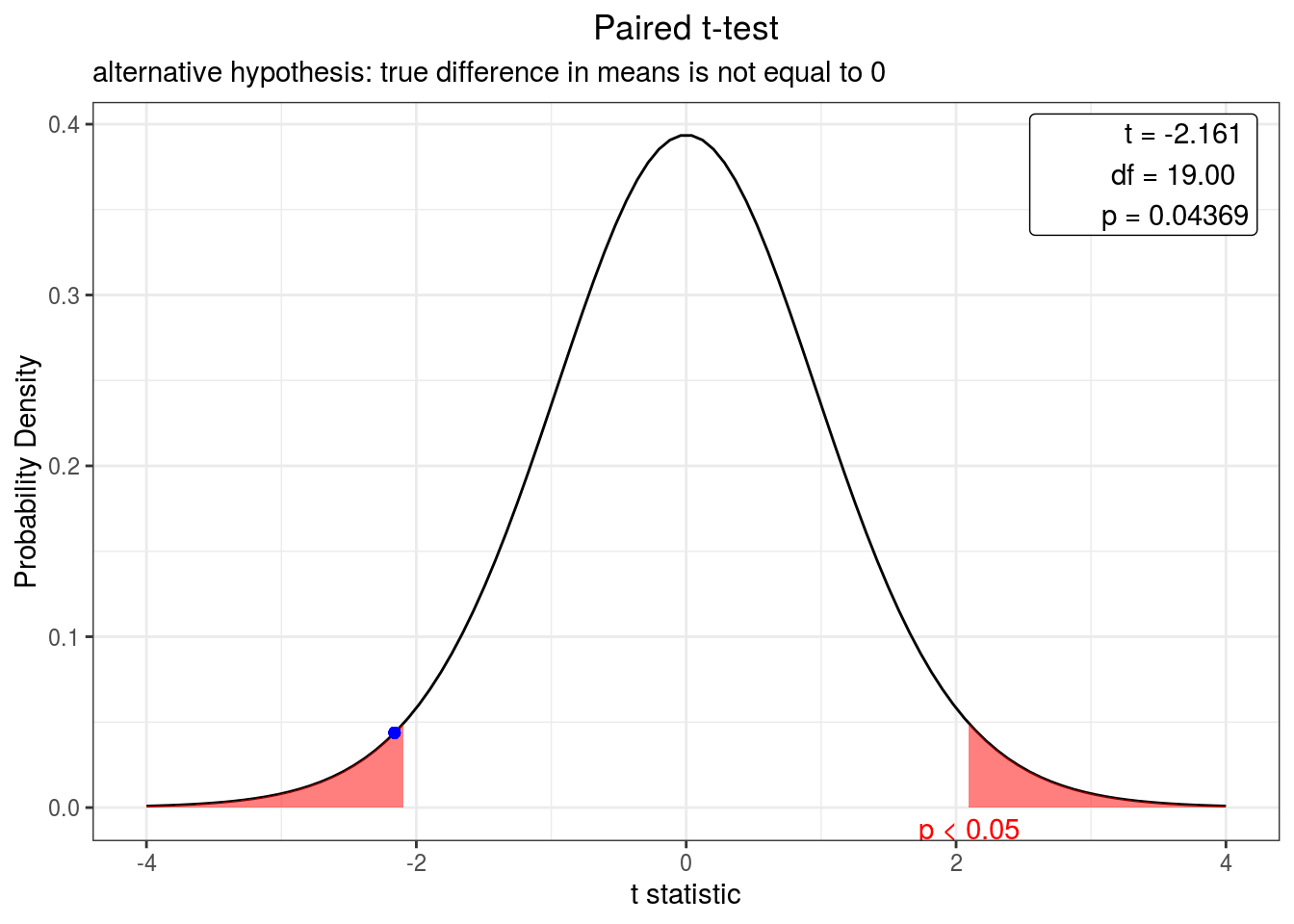
Figura 4.17: Curva de densidade representando o valor do teste-t bicaudal para comparação do número de observações de aves por 2 observadores distintos a um intervalo de confiança de 95%. O ponto azul indica o valor do teste.

Neste teste em particular como trabalhamos com a diferença entre as observações podemos usar o gráfico de barras para graficar essa diferença.

Para o gráfico indicaremos em seu comando que faremos um gráfico de barras onde o que será plotado é o objeto que consiste na diferença entre o número de observação de aves entre observadores (objeto: diferenca) (Figura 4.18). O argumento “xlab” indica o nome do eixo x, “ylab” o nome do eixo y, “main” indica o título do gráfico, “names.arg” indica a coluna referente aos nomes das barras (que são os dias), “las” indica se os nomes das barras serão plotados na horizontal ou vertical (o valor 2 indica vertical), “ylim” indica os limites do eixo y e “cex.names” indica o tamanho da letra dos nomes das barras.

barplot(diferenca,
        xlab = "Dias",
        ylab = "Diferença entre observadores (Observador 1 - Observador 2)",
        main = "Meu gráfico",
        names.arg = aves$Dia,
        las = 2,
        ylim = c(-7.3, 7.3),
        cex.names = 0.9)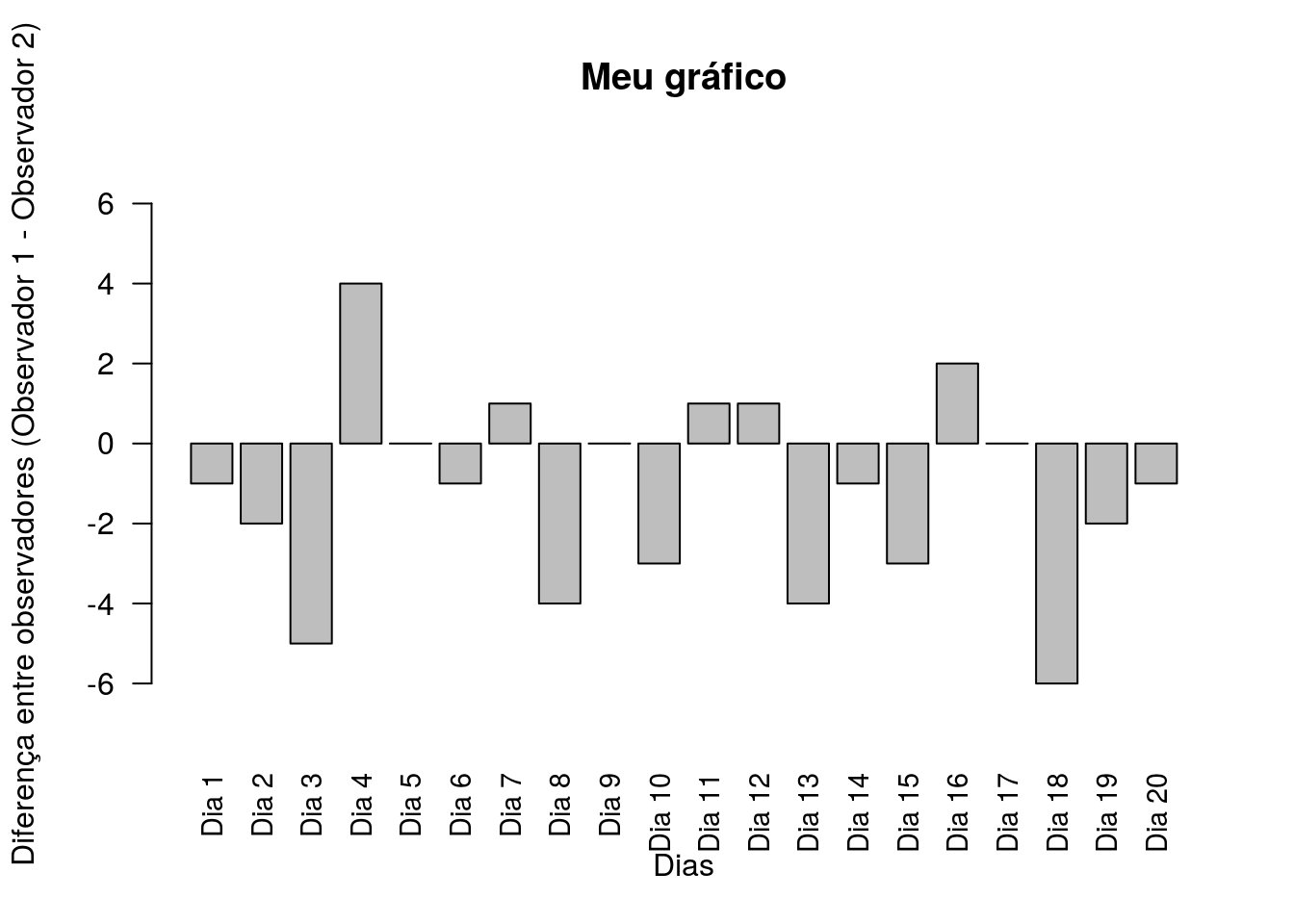

Figura 4.18: Diferença entre o número de observações de aves, por dia, para cada observador

As barras para o lado positivo do eixo y indica uma maior observação de aves pelo “Observador 1” e as barras para baixo indicam um maior número de observações de aves pelo “Observador 2”. Vamos indicar isso no gráfico por meio da função mtext() (Figura 4.19).

barplot(diferenca,
        xlab = "Dias",
        ylab = "Diferença entre observadores (Observador 1 - Observador 2)",
        main = "Meu gráfico",
        names.arg = aves$Dia,
        las = 2,
        ylim = c(-7.3, 7.3),
        cex.names = 0.9)
mtext(at = 4,
      line = -2,
      text = "Observador 1", 
      side = 3)
mtext(at = 4, 
      line = -2,
      text = "Observador 2", 
      side = 1)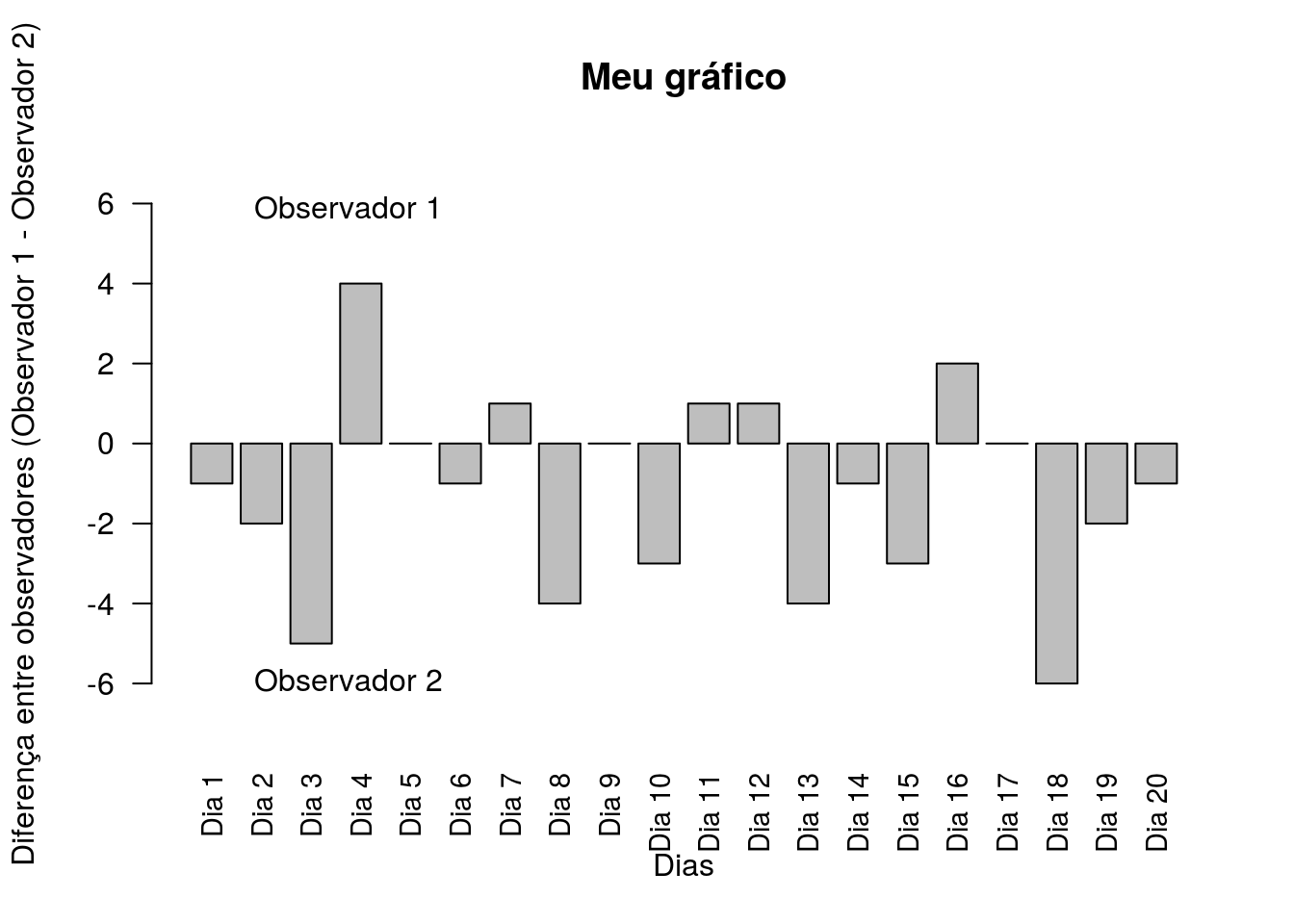

Figura 4.19: Diferença entre o número de observações de aves, por dia, para cada observador.

Como podem visualizar a função mtext() indicou os nomes “Observador 1” e “Observador 2” no lado do gráfico que os representa. O argumento “at” indica a posição em relação ao eixo x, “line” indica a posição em relação ao eixo y, “text” indica o que será plotado e side indica o lado da janela gráfica onde o texto será plotado (3 é na parte superior e 1 na inferior).

4.4 Considerações

Durante nosso percurso neste capítulo realizamos etapas que consistem na construção dos dados no próprio programa do R e a condução da análise do teste-t para uma amostra, para duas amostras e pareado. A construção dos dados tem como resultado final um objeto similar a planilha de dados que deve ser importada, caso já a tenha preparado, e juntamente com a sumarização dos dados temos as mesmas etapas trabalhadas no capítulo anterior. A partir daí temos a condução dos pressupostos normalidade e homocedasticidade e da análise estatística o teste-t. Um resumo gráfico das etapas pode ser observado aqui (Figura 4.20).

Figura 4.20: Resumo dos passos abordados no capítulo: da preparação dos dados até a análise dos dados.

4.5 Exercícios

1. Durante uma aula de biologia marinha, os alunos foram até um costão rochoso e realizaram amostragens não destrutivas da comunidade de organismos presentes na região entre marés. Foi observado ao final das amostragens os percentuais de algas a cada metro ao longo de um transecto de 20m. O resultado dos dados de algas, obtidos pelos alunos, pode ser obtido pela execução dos comandos abaixo:

set.seed(45)
algas <- (rnorm(n = 20, sd = 0.1) + runif(n = 20, min = 0, max = 0.8))*100

Na mesma aula oferecida à turma anterior, um ano antes no mesmo costão, foi observado uma média geral da população de algas de 52%. Usando seus conhecimentos sobre teste-t. Podemos dizer que o percentual de algas se manteve? Considere os níveis de confiança de 95% e 99%.

2. Qual foi o intervalo de confiança de 95% e 99% obtido no exercício anterior? A média de algas observada pela turma anterior (52%) encontra-se dentro ou fora destes intervalos?

3. Considerando o exemplo do exercício 1. Em um segundo momento a professora disponibilizou a turma os dados de algas obtidos pela turma anterior. Uma tabela com os dados de ambas as turmas pode ser obtido executando os comandos abaixo:

turmas <- c(rep(x = "turma.1", 20), rep(x = "turma.2", 20))
set.seed(44)
algas.turma1 <- (rnorm(n = 20, sd = 0.05) + runif(n = 20, min = 0.30, max = 0.83))*100
set.seed(45)
algas.turma2 <- (rnorm(n = 20, sd = 0.1) + runif(n = 20, min = 0, max = 0.8))*100
cobertura <- c(algas.turma1, algas.turma2)
algas.duasamostras <- as.data.frame(cbind(turmas, round(cobertura, 2)))
colnames(algas.duasamostras) <- c("turmas", "cobertura")
algas.duasamostras$turma <- as.factor(algas.duasamostras$turmas)
algas.duasamostras$cobertura <- as.numeric(algas.duasamostras$cobertura)
rm(list = "turmas", "algas.turma1", "algas.turma2", "cobertura")

Considerando, agora, o objeto algas.duasamostras. O que podemos dizer sobre o percentual de cobertura de algas, obtido por ambas as turmas, para os níveis de confiança de 95% e 99%? OBS: Converta as variáveis e conduza os pressupostos, se necessário.

4. Utilizando o objeto algas.duasamostras, do exercício anterior, realize um gráfico que demonstre o percentual obtido por cada turma contendo o desvio padrão.

5. Dois observadores independentes foram ao mesmo costão rochoso, anterior quantificaram a cobertura algal por metro, nos 20 metros do costão. Os dados obtidos por ambos os observadores pode ser obtido executando os comandos abaixo.

set.seed(235)
algas.observador1 <- (rnorm(n = 20, sd = 0.05) + runif(n = 20, min = 0.30, max = 0.83))*100
set.seed(236)
algas.observador2 <- (rnorm(n = 20, sd = 0.15) + runif(n = 20, min = 0.20, max = 0.80))*100
posicao <- seq(1:20)
algas.pareado <- as.data.frame(cbind(posicao, round(algas.observador1, 2), round(algas.observador2, 2)))
colnames(algas.pareado) <- c("posicao", "observador.1", "observador.2")
algas.pareado$observador.1 <- as.numeric(algas.pareado$observador.1)
algas.pareado$observador.2 <- as.numeric(algas.pareado$observador.2)
rm(list = "algas.observador1", "algas.observador2", "posicao")

De acordo com este novo objeto algas.pareado, o que podemos dizer sobre o percentual de cobertura de algas, em relação aos observadores para cada posição do costão, para os níveis de confiança de 95% e 99%? OBS: Conduza os pressupostos se necessário.

---

16. Consiste na subtração do nível de significância (alfa) de 1. Ou seja: nível de confiança = 1 - alfa.↩

17. por padrão o valor lógico para este argumento é FALSE e a função t.test() realiza o teste de Welch)↩

18. Zero (0) indica igualdade no número de observações.↩