A Resolução dos Exercícios

A.1 Capítulo 1

  1. b
  2. a
  3. c
  4. b
  5. e

A.2 Capítulo 2

  1. e
  2. d
  3. d
  4. b
  5. c

A.3 Capítulo 3

## 
##  Chi-squared test for given probabilities
## 
## data:  observados
## X-squared = 4.188, df = 1, p-value = 0.04071

De acordo com o resultado obtido p-value < 0,05, temos que o número decarros observados entre os períodos (manhã e tarde) são diferentes e de acordo com os valores obtidos (550 carros no período da manha e 620 no período da tarde) corroboramos corroboramos a observação do pesquisador que no período da tarde há um maior trafego de carros.

##       Quarta-feira Sexta-feira
## Manhã          200         350
## Tarde          230         390
## 
##  Pearson's Chi-squared test with Yates' continuity correction
## 
## data:  dados
## X-squared = 0.039543, df = 1, p-value = 0.8424

De acordo com o resultado obtido p-value > 0,05, não podemos refutar a hipótese nula (H0: As proporções relativas da circulação de carros na praia por período do dia são independentes dos dias da semana avaliados).

##       Quarta-feira Sexta-feira
## Manhã     46.51163     47.2973
## Tarde     53.48837     52.7027

  1. O erro tipo 1 consiste em rejeitar a hipótese nula quando ela é verdadeira. O erro tipo 2 consiste em aceitar a hipótese nula quando ela é falsa. No exercício 2 o p-value obtido foi de 0,057, o que corrobora a hipótese nula (H0), a um nível de confiança de 95%. Neste caso, como o nível de significância é próximo do limite estabelecido, há o risco de cometer o erro tipo 2.

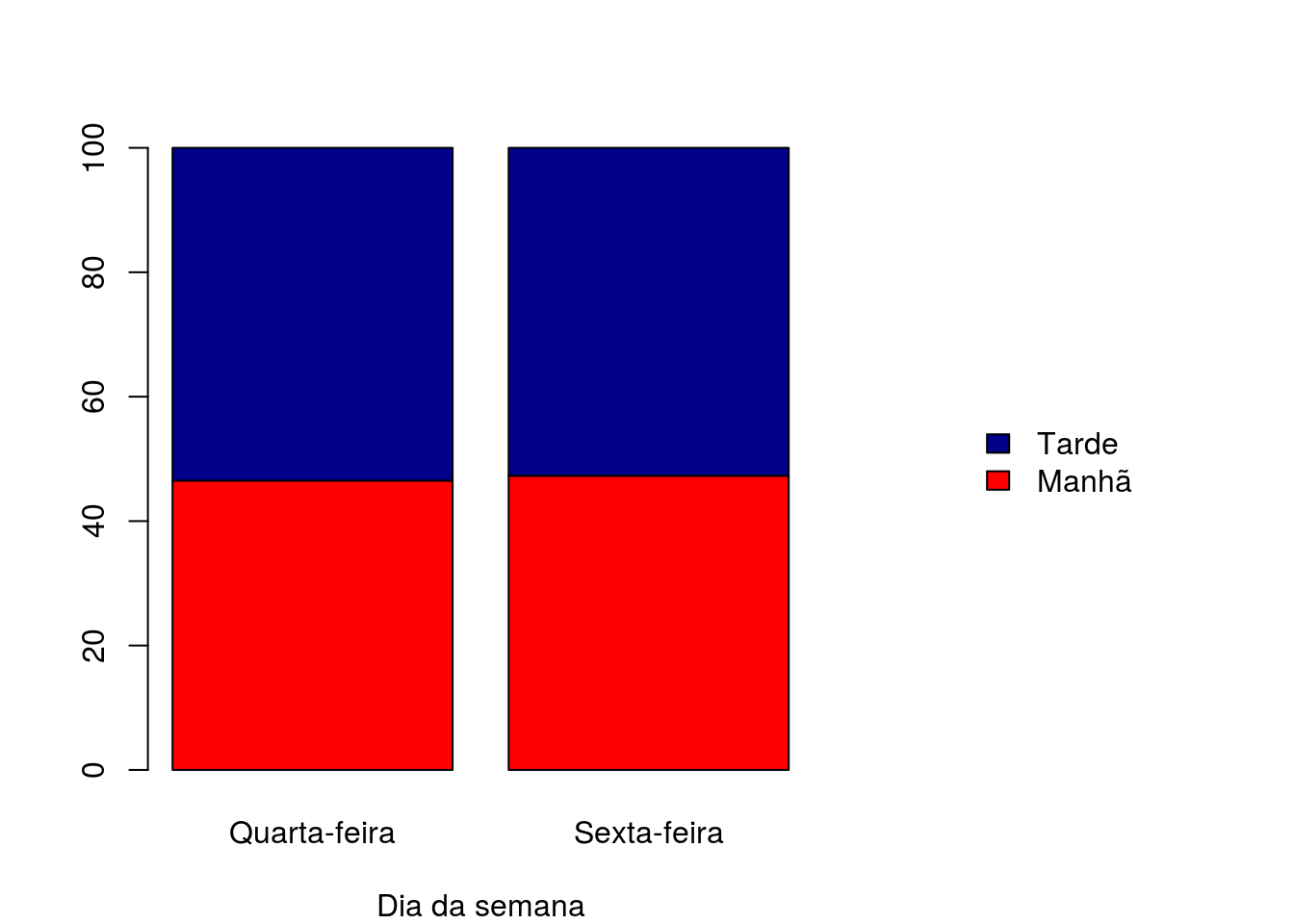
A.4 Capítulo 4

## 
##  One Sample t-test
## 
## data:  algas
## t = -2.5378, df = 19, p-value = 0.02007
## alternative hypothesis: true mean is not equal to 52
## 95 percent confidence interval:
##  30.11439 49.89807
## sample estimates:
## mean of x 
##  40.00623
## 
##  One Sample t-test
## 
## data:  algas
## t = -2.5378, df = 19, p-value = 0.02007
## alternative hypothesis: true mean is not equal to 52
## 99 percent confidence interval:
##  26.48517 53.52730
## sample estimates:
## mean of x 
##  40.00623

A depender do nível de confiança podemos ter diferentes conclusões. Se considerarmos um nível de confiança de 95% podemos dizer que a média do percentual de algas obtido pela turma que foi de 40,01% difere da média obtida pela turma anterior que foi de 52% com um p-value de 0,02. Se considerarmos um nível de confiança de 99% podemos dizer que a média do percentual de algas obtido pela turma que foi de 40,01% é similar ao obtido pela turma anterior que foi de 52% com um p-value de 0,02.

  1. O intervalo de confiança para o nível de 95% encontra-se entre: 30,11 e 49,90. O valor de 52% encontra-se fora do intervalo de confiança; O intervalo de confiança para o nível de 99% encontra-se entre: 26,49 e 53,53. O valor de 52% encontra-se dentro do intervalo de confiança;

## 
##  Shapiro-Wilk normality test
## 
## data:  algas.duasamostras$cobertura[algas.duasamostras$turmas == "turma.1"]
## W = 0.91597, p-value = 0.08291
## 
##  Shapiro-Wilk normality test
## 
## data:  algas.duasamostras$cobertura[algas.duasamostras$turmas == "turma.2"]
## W = 0.97976, p-value = 0.9309
## 
##  Bartlett test of homogeneity of variances
## 
## data:  cobertura by turmas
## Bartlett's K-squared = 2.2754, df = 1, p-value = 0.1314
## 
##  Two Sample t-test
## 
## data:  cobertura by turmas
## t = 2.0497, df = 38, p-value = 0.04734
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##   0.146276 23.522724
## sample estimates:
## mean in group turma.1 mean in group turma.2 
##               51.8420               40.0075
## 
##  Two Sample t-test
## 
## data:  cobertura by turmas
## t = 2.0497, df = 38, p-value = 0.04734
## alternative hypothesis: true difference in means is not equal to 0
## 99 percent confidence interval:
##  -3.821193 27.490193
## sample estimates:
## mean in group turma.1 mean in group turma.2 
##               51.8420               40.0075

Ambas os conjuntos de dados demonstraram normalidade, pelo teste de Shapiro-Wilks, assim como homocedasticidade das variâncias, pelo teste de Bartlett. O teste-t fornece um p-value de 0,04734. Ao considerar o nível de confiança de 95% temos o valor no limiar da rejeição da hipótese nula. Se considerarmos o p-value como <0,05 podemos refutar a hipótese nula e dizer que a cobertura algal obtida pelas duas turmas é diferente. Contudo ao nível de confiança de 99% podemos corroborar a hipótese nula e dizer que a cobertura algal observada por ambas as turmas são similares, embora a média de cobertura obtida pela primeira turma seja 11% menor.

## 
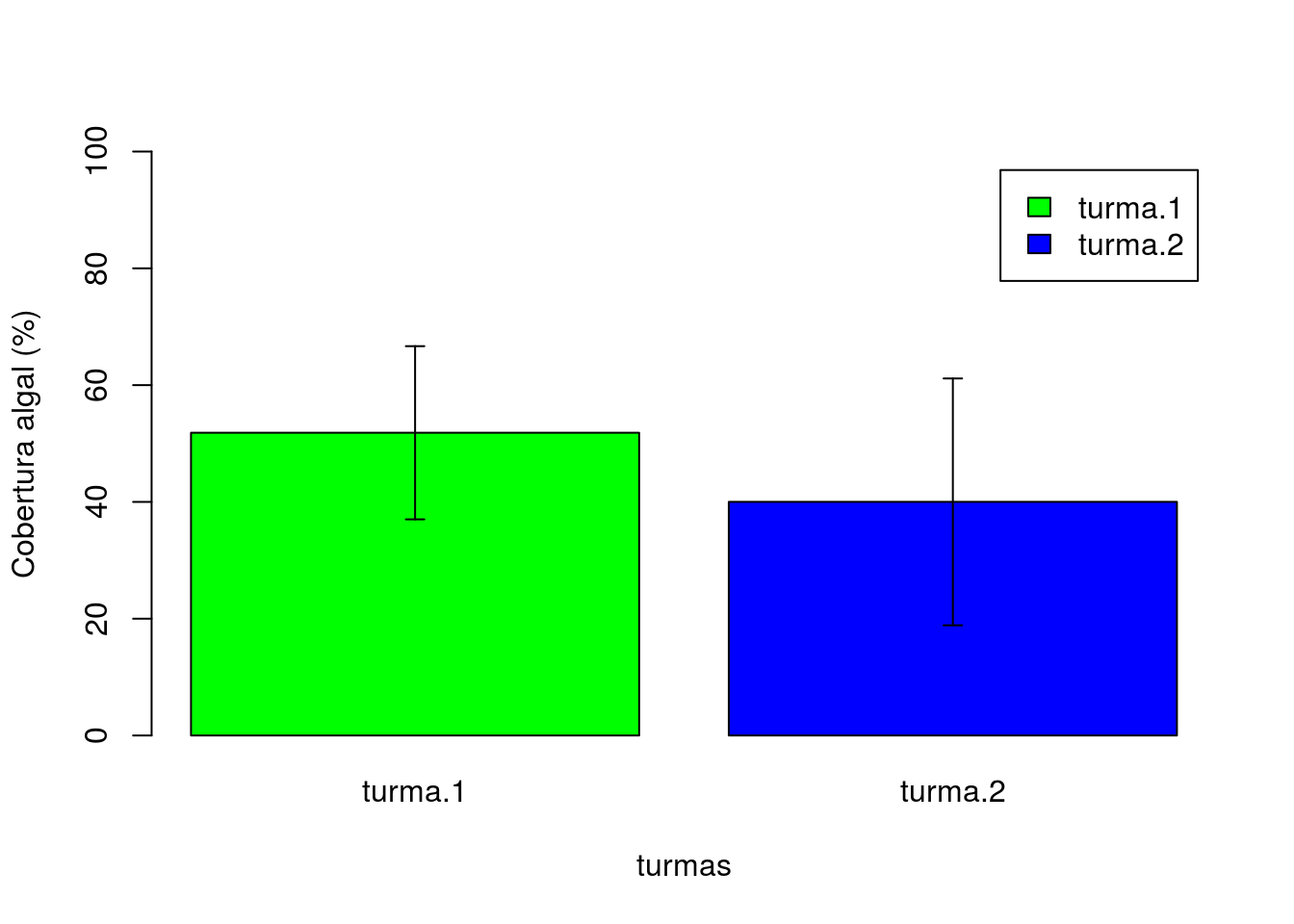
##  Shapiro-Wilk normality test
## 
## data:  diferenca
## W = 0.96839, p-value = 0.7206
## 
##  Paired t-test
## 
## data:  algas.pareado$observador.1 and algas.pareado$observador.2
## t = 0.91619, df = 19, p-value = 0.3711
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -7.052518 18.033518
## sample estimates:
## mean of the differences 
##                  5.4905
## 
##  Paired t-test
## 
## data:  algas.pareado$observador.1 and algas.pareado$observador.2
## t = 0.91619, df = 19, p-value = 0.3711
## alternative hypothesis: true difference in means is not equal to 0
## 99 percent confidence interval:
##  -11.65443  22.63543
## sample estimates:
## mean of the differences 
##                  5.4905

A diferença entre os observadores mostrou normalidade para o teste de Shapiro-Wilks e independente do nível de confiança adotado (95% ou 99%) a média da diferença foi proxima a 0, indicando similaridade entre as observações. Corroborando, portanto, a hipótese nula (H0), de que não há diferença entre os observadores.