Capítulo 3 Qui-quadrado (\(\chi\)²)

Até o momento aprendemos a definir o ambiente em que iremos trabalhar, importar nossa planilha, verifica-la e ajusta-la se necessário, assim como as métricas mais utilizadas para sumarizar os dados. Mas por vezes estamos interessados em analisar os dados, então vamos começar com o Qui-quadrado.

Em alguns momentos podemos estar trabalhando com variáveis categóricas e lidarmos com perguntas sobre estas variáveis e portanto pode ser necessário avaliarmos se a frequência das observações de uma dada variável categórica ajusta-se ao que se é esperado (\(\chi\)² para ajuste de frequências) ou se as proporções das observações de duas ou mais variáveis categóricas são independentes uma da outra (\(\chi\)² para independência).

De modo que, para este teste iremos precisar apenas de uma variável (se estivermos avaliando o ajuste de frequências) ou duas variáveis (se avaliarmos a independência) e estas devem ser categóricas. Como aprendemos anteriormente as variáveis categóricas devem ser classificadas como fator (pela função as.factor()) no R. Vamos conferir em detalhes e com exemplos como realizar estas duas análises no R.

3.1 \(\chi\)² para ajuste de frequências

Tabela 3.1: Principais características do qui-quadrado para ajuste das frequências
Atributos Características
Tipo de variável Categórica
Quantidade de variáveis 1
Hipótese nula O número de observações em cada grupo da variável é similar ao predito pela teoria
Fórmula \[\chi^2=\sum^{N}_{i = 1}\frac{(Ob-Es)^2}{Es}\]
Observação Se há apenas 2 categorias, dentro da variável, não há a necessidade de post-hoc nem expressa-la graficamente

Imagine o seguinte exemplo: Você foi a praia e verificou uma enorme quantidade de produtos plásticos, esquecidos pelas pessoas. Após um tempo de observação você percebeu que haviam tanto sacolas quanto tampas de garrafa PET e poderia levantr a seguinte pergunta: Será que se coletarmos estes plásticos na praia e o categorizarmos eles apresentarão quantidades similares? A partir desta pergunta a seguinte hipótese nula (H0) é naturalmente construída: Não há diferenças entre estes dois tipos de plásticos (tampas e sacolas). O \(\chi\)² objetiva responder a essa pergunta e fornecer subsídio estatístico para corroborar ou refutar essa hipótese.

Após a observação, coleta, classificação e contagem dos fragmentos plásticos os seguintes valores foram observados: 520 sacolas plásticas e 470 tampas. Dessa forma podemos perguntar: do total de fragmentos coletados (520 para sacolas e 470 para tampas) cada um deles contribuem com 50% (percentuais iguais) do total?

Vamos começar criando 2 vetores13 onde o primeiro corresponde aos valores observados e o segundo as proporções esperadas para cada valor.

## [1] 520 470
## [1] 0.5 0.5

Note que criamos os objetos “observados” e “esperados”. O primeiro corresponde ao que coletamos e o segundo as proporções que esperamos de ambos.

Para realizar o teste do \(\chi\)² para ajuste de frequências, vamos utilizar a função chisq.test().

## 
##  Chi-squared test for given probabilities
## 
## data:  observados
## X-squared = 2.5253, df = 1, p-value = 0.112

Esta função utiliza 2 argumentos: * x: no qual inserimos o vetor númerico que contém os valores referentes a quantidade da variável nominal que contabilizamos; * p: no qual inserimos o vetor númerico que contem as proporções esperadas associado a cada grupo da categoria avaliada.

Note que o resultado indica o teste realizado, o nome do objeto que contém os dados e na terceira linha ele apresenta o resultado como valor do teste do \(\chi\)², o grau de liberdade (df do inglês degrees of freedom) e o valor de probabilidade associado (do inglês p-value).

Uma característica do \(\chi\)² é que quanto mais similares forem os valores observados menor será o valor do \(\chi\)², mas nunca menor que 0 e com o p-value máximo igual a 1 e quanto mais dissimilares forem os valores observados maior será o \(\chi\)² (tendendo a infinito) e menor será o p-value (tendendo a 0)

Com isso podemos observar que o \(\chi\)² varia entre (0 e + infinito) enquanto que o p-value varia entre (0 e 1) com uma relação inversa entre eles. Quanto maior o \(\chi\)² menor o p-value e quanto menor o \(\chi\)² maior o p-value.

Por convenção indicamos que um teste estatístico que apresenta p-value < 0,05 indica diferenças significativas entre os valores observados. Dessa forma, assumindo essa convenção, podemos concluir que a quantidade de sacolas não difere da quantidade de tampas de garrafa PET. Portanto aceitamos a hipótese nula.

Não é comum representar o resultado deste teste graficamente apenas como valor mas se mesmo assim quiser representa-lo utilize um gráfico de barras.

Vamos verificar outros exemplos e avaliar suas hipóteses nulas.

Imagine um segundo exemplo. 300 flores foram fotografadas e classificadas pela cor e ao final foi obtido um total de 170 flores vermelhas e 130 flores verdes. Ao ler alguns trabalhos e analisar os resultados observados para outra região foi levantada a hipótese de que 70% das flores seriam vermelhas e 30% seriam verdes. Com base nesses dados podemos perguntar: As flores fotografadas confirmam os resultados esperados?

Vamos avaliar este caso, conforme fizemos acima.

Observe que igual nosso exemplo anterior criamos objetos flores.observadas e flores.esperadas. Note que a diferença está nos valores esperados, onde alteramos a proporção, que não é mais de 50% para cada, mas sim de 70% para um e 30% para outro, porém expressos em proporção (valores variam entre 0 e 1). Perceba, também, que os valores seguem a ordem em que foram inseridos, portanto o primeiro valor observado inserido corresponde ao primeiro valor esperado inserido e assim por diante.

Ao conduzir a análise temos o seguinte resultado

## 
##  Chi-squared test for given probabilities
## 
## data:  flores.observadas
## X-squared = 25.397, df = 1, p-value = 4.667e-07

Perceba que o valor do \(\chi\)² aumentou em relação ao exemplo anterior e o p-value diminuiu para um valor bem próximo a 0. Este resultado indica que os valores observados de flores vermelhas e verdes não apresentam as proporções que se esperam de 70% e 30%. Portanto refutamos a hipótese nula de que elas se encontram nas proporções esperadas.

Vamos seguir em frente e olhar para um outro exemplo. Suponha que foram coletados 2660 indivíduos de siri em um estuário. Eles foram classificados em relação ao sexo e foram obtidos 1380 fêmeas e 1280 machos. Espera-se que a razão sexual desta espécie seja de 1:1 (50% para cada sexo). Os indivíduos amostrados confirmam o que é esperado?

## 
##  Chi-squared test for given probabilities
## 
## data:  siris.observados
## X-squared = 3.7594, df = 1, p-value = 0.05251

Com este caso podemos observar que o valor do \(\chi\)² indicou um p-value próximo a 0,05, indicando que temos de ter cuidado com as afirmações relativas a hipótese testada. Contudo, como o valor é >0,5 podemos corroborar a hipotese nula e dizer que os valores observados para fêmeas e machos encontram-se dentro da proporção esperada de 1:1.

E se ao invés de 2 grupos tivessemos 3 ou mais. Como realizariamos o \(\chi\)²? Vamos ver com um exemplo.

Imagine que você foi a uma floresta e classificou as árvores em altas, médias e baixas e contabilizou 55, 31 e 27 respectivamente. De acordo com a literatura é esperado que as proporções de árvores altas, médias e baixas seja de 1:1:1. Vamos analisar e verificar se podemos afirmar que o observado corrobora o esperado.

## 
##  Chi-squared test for given probabilities
## 
## data:  arvores.observadas
## X-squared = 12.177, df = 2, p-value = 0.002269

Neste exemplo podemos perceber que a análise é igual a todos os casos anteriores, a diferença é que adicionamos um grupo a mais e consequentemente um valor a mais. Devido a essa mudança tivemos que dividir as probabilidades (objeto arvores.esperadas) em 3 valores e de igual probabilidade, já que o hipotetizado consistia em proporções iguais para os três grupos definidos. De acordo com o resultado obtido podemos perceber que o que foi observado não corrobora o esperado.

Vamos observar quais seriam as quantidades de árvores esperadas de acordo com as quantidades que observamos e as proporções que esperamos.

Para isso precisamos primeiramente inserir o resultado em um objeto e a seguir acessar os componentes desse objeto pelo operador matemático $ (cifrão), seguido pelo objeto expected criado pela função chisq.test().

## [1] 37.66667 37.66667 37.66667

Os exemplos acima tratam de avaliar o \(\chi\)² em variáveis que apresentam dois ou mais grupos. Quando o grau de liberdade é 1 (dois grupos) e o número de observações é considerado baixo é sugerido a aplicação da correção de Yates. Quando o número de observações é elevado ela não distorce o resultado. O risco de se usar o \(\chi\)² sem a correção de Yates consiste em inflar o valor de \(\chi\)² e portanto diminuir o p-value o que nos levaria ao risco de rejeitarmos a hipótese nula quando ela é verdadeira (erro tipo I).

A função do \(\chi\)², no pacote base do R, não realiza a correção de Yates para este teste, apenas para o próximo caso que iremos tratar (\(\chi\)² para independência). Contudo ele oferece outro método para avaliação deste teste que consiste na simulação de Monte Carlo. Não entraremos em detalhes de como funciona este teste, mas o que alertamos é que se o número de observações utilizado é considerado baixo correções devem ser aplicadas. Embora os cálculos envolvidos para realização da correção de Yates não seja complicada sugerimos a leitura da literatura especializada.

Vamos verificar um exemplo onde a correção de Monte Carlo, a qual é possível de ser realizada de maneira rápida e prática no R, é aplicada.

Imagine que você foi em campo e contabilizou as espécies de cracas que identificou. Foram contabilizados 12 cracas da espécie A e 24 da espécie B. Trabalhos anteriores demonstraram que ambas as espécies encontram-se na proporção de 1:1. Aplicando a simulação de Monte Carlo o número de indivíduos observados de ambas as espécies corroboram o esperado?

## 
##  Chi-squared test for given probabilities
## 
## data:  N.especies
## X-squared = 4, df = 1, p-value = 0.0455
## 
##  Chi-squared test for given probabilities with simulated p-value (based
##  on 2000 replicates)
## 
## data:  N.especies
## X-squared = 4, df = NA, p-value = 0.06347

Basta usarmos o argumento “simulate.p.value” e indicar “FALSE” quando não queremos a simulação de Monte Carlo, ou apenas omitirmos este argumento, ou usar este argumento e indicar “TRUE” o qual realiza a simulação de Monte Carlo. Verifique que com a aplicação desta simulação o p-value aumenta indicando que torna mais dificil rejeitarmos a hipótese nula. Após aplicarmos a correção na nossa análise podemos afirmar que não há diferença na quantidade de cracas observadas em relação as proporções esperadas, para ambas as espécies de cracas.

Relembrando. Sempre tome cuidado com afirmações! Principalmente quando o número de observações é baixo. Mesmo que o teste estatístico indique diferenças, uma baixa quantidade de observações devem ser analisadas cuidadosamente, no entanto devemos aplicar correções matemáticas nestes casos.

3.2 \(\chi\)² para independência

Realizamos este teste quando objetivamos saber se a frequência dos grupos de uma variável é independente de outra variável.

Diferente do primeiro caso de \(\chi\)² que abordamos, este lida com duas variáveis categóricas ao invés de uma. Portanto é necessário o desenvolvimento de uma tabela de contigência.

A tabela de contigência consiste em uma tabela com o número de observações referentes as duas variáveis selecionadas. Veremos alguns exemplos abaixo.

Para o momento. Veja o sumário abaixo no qual detalhamos as principais características desta análise.

Tabela 3.2: Principais características do qui-quadrado para independência
Atributos Características
Tipo de variável Categórica.
Quantidade de variáveis 2 ou mais.
Hipótese nula As proporções relativas de uma variável são independentes de uma segunda variável.
Fórmula Para uma tabela 2 $$2 temos: \[\chi^{2} = \frac{n(f_{11}f_{22}-f_{12}f_{21})^2}{R_{1}R_{2}C_{1}C_{2}}\] Onde n é onúmero total de observações; \(f_{11}\) é o valor da primeira linha e primeira coluna; \(f_{22}\) é o valor da segunda linha e segunda coluna; \(f_{12}\) é o valor da primeira linha e da segunda coluna; \(f_{21}\) é o valor da segunda linha e primeira coluna; \(R_{1}\) é a soma da primeira linha; \(R_{2}\) é a soma da segunda linha; \(C_{1}\) é a soma da primeira coluna e \(C_{2}\) é a soma da segunda coluna.
Observação Como característica intrinseca a este teste é necessário a construção da tabela de contigência.

Imagine a seguinte situação: Insetos foram coletados, ao acaso, em uma região costeira. Todos os insetos foram avaliados quanto a espécie e a presença de parasitas. Os seguintes valores foram obtidos: 55 indivíduos da espécie A com parasita, 75 indivíduos da espécie A sem parasita, 90 indivíduos da espécie B com parasita e 110 indivíduos da espécie B sem parasita. Foi levantada a hipótese nula de que a quantidade de indivíduos infectados pelo parasita é o mesmo para ambas as espécies.

Vamos começar criando uma matriz14 com esses valores, onde as linhas corresponderão as espécies, as colunas a presença/ausência do parasita e os seus elementos corresponderão a quantidade de indivíduos dada as condições (espécie e parasita).

Para construir nossos dados utilizaremos a função matrix, com os argumentos “data”, onde adicionaremos os elementos que estarão presentes, “ncol” onde definiremos a quantidade de colunas e “byrow” onde definiremos que os valores presentes no argumento “data” serão inseridos em ordem por linha, neste caso a função começará preenchendo a primeira linha da primeira coluna, segunda linha da primeira coluna, primeira linha da segunda coluna e segunda linha da segunda coluna. Guardaremos nossa matriz criada em um objeto chamado dados. Utilizaremos as funções rownames() e colnames() a fim de definir os nomes das linhas e colunas da nossa matriz para melhor visualização. A seguir iremos visualizar o objeto dados.

##           Com parasita Sem parasita
## Espécie A           55           75
## Espécie B           90          110

Pronto nossa tabela de contigência está criada. Vamos seguir para a análise

## 
##  Pearson's Chi-squared test with Yates' continuity correction
## 
## data:  dados
## X-squared = 0.13543, df = 1, p-value = 0.7129

Ao executarmos a função chisq.test() utilizando apenas a matriz como objeto do argumento “x” ele nos retorna o \(\chi\)² com a correção de Yates. O que é sugerido para quando estamos lidando com matrizes \(2 \times 2\). No geral o resultado é similar ao que executamos no tópico anterior.

Uma atenção deve ser dada ao grau de liberdade o qual indica o valor de 1. O cálculo do grau de liberdade consiste no número de linhas menos um multiplicado pelo número de colunas menos um. Como temos 2 linhas e 2 colunas o grau de liberdade será: \((2-1)*(2-1) = 1*1 = 1\).

De acordo com o resultado obtido pelo teste não podemos refutar nossa hipótese nula. Portanto dizemos que a proporção da população infectada pelo parasita é a mesma nas duas espécies.

Vejamos um segundo exemplo.

Durante 2 anos camarões foram coletados, em um estuário, e todos eles foram sexados em machos e fêmeas. Objetivou-se com esses dados saber se há algum desvio da razão sexual entre os anos.

Vamos começar desenvolvendo um conjunto de dados na forma de planilha, que é como seus dados devem estar planilhados e vamos ensina-lo a construir uma tabela de contingência a partir desses dados.

Execute o código abaixo. Não se preocupe, no momento, com as funções novas utilizadas. A única função diferente é rep() que repete um determinado elemento n vezes. No código abaixo, estaremos repetindo o elemento “Ano 1” 150 vezes e o elemento “Ano 2” 225 vezes e concatenaremos estes elementos por meio da função c() e guardando-o no objeto ano faremos o mesmo para o objeto sexo onde concatenaremos a repetição do elemento “macho” 55 vezes, seguido por “fêmea” 95 vezes, seguido novamente por “macho” 105 vezes e por fim “fêmea” 120 vezes. Após isso uniremos os dois objetos ano e sexo por meio da função cbind() e diremos que isso consiste em um objeto da classe data frame por meio da função data.frame() e guardaremos esse resultado em um objeto denominado dados.

Vamos visualizar nossos dados. Para isso podemos usar a função head() que mostra no console as primeiras linhas desse data frame.

##     ano  sexo
## 1 Ano 1 macho
## 2 Ano 1 macho
## 3 Ano 1 macho
## 4 Ano 1 macho
## 5 Ano 1 macho
## 6 Ano 1 macho

Agora vamos, a partir de dados construir uma tabela de contigência. Para isso vamos utilizar a função table() e guardar seu resultado em um objeto chamado tab.cont. A seguir iremos visualizar nossa tabela de contingência chamando tab.cont

##        sexo
## ano     fêmea macho
##   Ano 1    95    55
##   Ano 2   120   105

Vamos agora realizar o qui-quadrado de nossos dados.

## 
##  Pearson's Chi-squared test with Yates' continuity correction
## 
## data:  tab.cont
## X-squared = 3.2817, df = 1, p-value = 0.07006

Pronto! Como podem ver, a representação do resultado é similar ao exemplo acima. Contudo nossos dados são diferentes e portanto nossa hipótese nula é diferente.

Nossa hipótese nula pode ser escrita de três formas. Vejamos os 3 exemplos abaixo:

  • H0: Na população amostrada a proporção de machos e fêmeas é independente do ano;
  • H0: Na população amostrada a razão sexual dos camarões é a mesma entre os anos;
  • H0: A proporção de camarões entre os anos é a mesma para ambos os sexos;

Como o teste resultou em um p-value maior que 0,05 podemos dizer, por essa via, que corroboramos nossa hipótese nula.

Neste ponto é bom relembramos da importância do número de observações de cada grupo. Se este número for pequeno, incertezas podem ser geradas e ajustes devem ser feitos. Contudo, para definir o que é um número baixo de observações sigamos para o cálculo sugerido por Zar (2010)15 o qual define como: \(n = 6rc\).

Onde, n é o número de observações mínimo de cada grupo, r é o número de linhas (rows) e c é o número de colunas (column). Dessa forma, em uma tabela de contigência do tipo \(2 \times 2\) o número de observações mínimo para cada grupo deve ser de: \(n = 6 \times (2) \times (2) = 24\). Ou seja, 24 observações.

Esta análise pode ser conduzida, também, quando lidamos com mais de um grupo em uma categoria e neste caso teriamos uma tabela de contigência \(2 \times 3\), \(2 \times 4\), \(3 \times 3\) e assim por diante. Vamos ver um exemplo.

Três pesquisadores analisaram fotografias de espécies bentônicas em um costão objetivando avaliar a abundância de duas espécies, uma introduzida e uma nativa. Considere todo o processo amostral similar e que os pesquisadores avaliaram as mesmas fotografias. Neste caso nossa hipótese nula é que a proporção entre as espécies é similar independentemente dos pesquisadores.

Vamos construir nossa matriz de uma outra forma.

##                     pesquisador 1 pesquisador 2 pesquisador 3
## Espécie nativa                 70            79            38
## Espécie introduzida            84            95            80

Os dados foram construídos passo a passo. Vamos analisar e verificar o resultado.

## 
##  Pearson's Chi-squared test
## 
## data:  dados
## X-squared = 6.2322, df = 2, p-value = 0.04433

Repare que há algo diferente, como realizamos a análise em uma tabela \(2 \times 3\) por padrão a função chisq.test() não realiza a correção de Yates. Pois não é necessário.

Analisando o resultado podemos inferir que as proporções observadas de espécies nativas e introduzidas são diferentes em função do pesquisador. Ou seja, rejeitamos nossa hipótese nula de que as proporções são similares. Contudo o p-value foi bem próximo ao limiar de 0,05. Podemos nos aprofundar na questão e nos perguntar onde está essa diferença? Entre o pesquisador 1 e o pesquisador 2 ou entre outra dupla de pesquisadores? Como observamos isso?

Para responder essa pergunta em específico, vamos subdividir nossa tabela de contigência para todos os pares de observações e armazena-los em outros objetos.

Para isso criaremos tabelas \(2 \times 2\) para cada par de comparações. Repare que usaremos a nossa tabela dados originalmente criada seguida por colchetes e dentro do colchetes inserimos virgula e menos o número referente a coluna. O colchetes após o nome dos dados nos permite acessar as linhas e colunas de um conjunto de dados quaisquer com isso podemos remove-las ou seleciona-las. Qualquer número antes da virgula indica a linha e qualquer número após a vírgula indica a coluna. O sinal de menos indica que vamos remover e se não colocarmos sinal indica que iremos selecionar o valor especificado. No primeiro caso onde inserimos “-3” após a virgula estamos indicando que vamos remover a terceira coluna do objeto dados e armazenar este resultado em um novo objeto chamado p1.p2. O mesmo raciocínio segue nos demais casos.

Sabendo isso vamos realizar a função chisq.test() para cada par de observações e analisar seu resultado.

## 
##  Pearson's Chi-squared test with Yates' continuity correction
## 
## data:  p1.p2
## X-squared = 0, df = 1, p-value = 1
## 
##  Pearson's Chi-squared test with Yates' continuity correction
## 
## data:  p1.p3
## X-squared = 4.3623, df = 1, p-value = 0.03674
## 
##  Pearson's Chi-squared test with Yates' continuity correction
## 
## data:  p2.p3
## X-squared = 4.5663, df = 1, p-value = 0.03261

Repare que não há diferenças entre a proporção de espécies observadas entre os pesquisadores 1 e 2. Mas entre o pesquisador 3 e os demais há diferença. Isto indica que é o pesquisador 3 que destoa dos demais em relação a observação de espécies nativas e introduzidas.

Quando observamos todo o conjunto de dados não observamos esta característica, mas ao separarmos os dados a diferença fica evidenciada.

Uma prática comum nesta análise é demonstrar o resultado por meio gráfico. Portanto, vamos observar como representar graficamente este último exemplo.

Primeiro vamos transformar nossa tabela de contigência em uma tabela no qual os valores irão corresponder a proporções relativas. Para isso vamos usar a função prop.table() e armazenar este resultado em um objeto chamado tabela.

##                     pesquisador 1 pesquisador 2 pesquisador 3
## Espécie nativa          0.1569507     0.1771300    0.08520179
## Espécie introduzida     0.1883408     0.2130045    0.17937220

Como podem ver o resultado deste nosso passo nos retornou uma tabela de proporções em relação ao total. Podemos transformar-la em percentual, basta multiplicarmos a tabela por 100. Vamos ver o processo

##                     pesquisador 1 pesquisador 2 pesquisador 3
## Espécie nativa           15.69507      17.71300      8.520179
## Espécie introduzida      18.83408      21.30045     17.937220

Pensando um pouco na nossa análise e no que ela avalia. O \(\chi\)² está avaliando as proporções relativas entre os grupos de uma dada variável, neste último caso a proporção das espécie em relação aos pesquisadores. Então a tabela de proporções ou percentual que nos interessa é a relação entre a espécie nativa e introduzida por pesquisador. A função prop.table() nos permite definir isso por meio do argumento “margin”, vamos verificar o resultado olhando para o resultado em percentual.

##                     pesquisador 1 pesquisador 2 pesquisador 3
## Espécie nativa           37.43316      42.24599      20.32086
## Espécie introduzida      32.43243      36.67954      30.88803
##                     pesquisador 1 pesquisador 2 pesquisador 3
## Espécie nativa           45.45455       45.4023      32.20339
## Espécie introduzida      54.54545       54.5977      67.79661

Como podem visualizar, se usarmos “margin = 1” ele nos retorna os valores em função das linhas (espécies), se utilizarmos “margin = 2” ele nos retorna os valores em função das colunas (pesquisadores).

Vamos utilizar “margin = 2” para construir nossa tabela e plotarmos nosso gráfico (Figura 3.1).

Gráfico de barras sobrepostas indicando o percentual relativo da observação de espécies nativas (cor vermelha) e introduzidas (cor azul), por pesquisador.

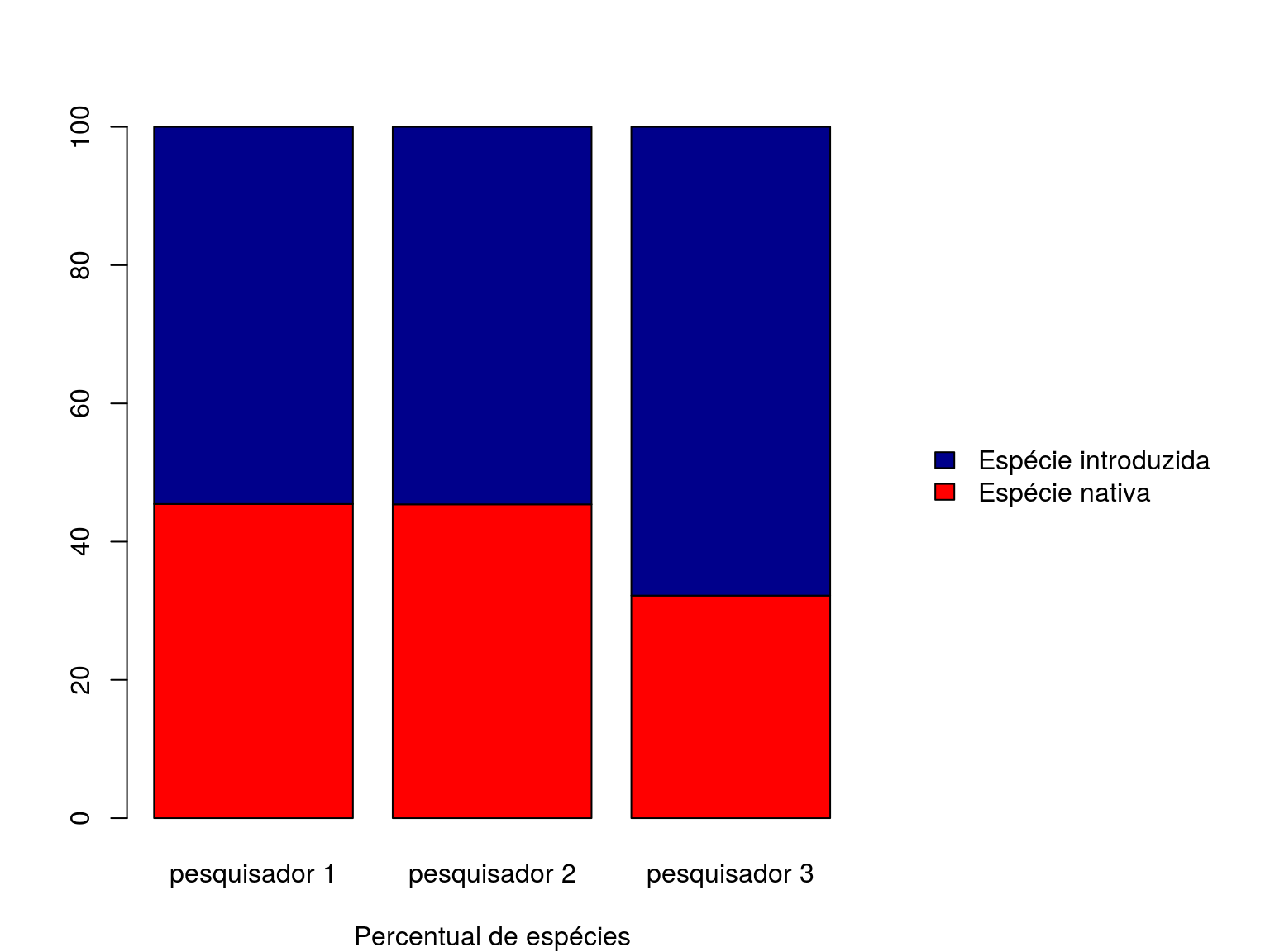
Figura 3.1: Gráfico de barras sobrepostas indicando o percentual relativo da observação de espécies nativas (cor vermelha) e introduzidas (cor azul), por pesquisador.

Como podem ver o nosso gráfico foi realizado. Mas adicionamos uma série de comandos novos. Vamos explica-los passo a passo.

Primeiro contruímos a tabela com os dados em percentuais relativos ao pesquisador e o armazenamos em um objeto chamado tabela.

Posteriormente utilizamos uma função chamada par() com o argumento “mar” no qual concatenamos 4 valores. Esta função juntamente com esse argumento permite que redimensionemos a janela gráfica. Os quatro valores concatenados referem-se as margens inferior, esquerda, superior e direita, respectivamente.

Nosso último passo é a nossa já conhecida função barplot(), onde inserimos como primeiro valor o objeto que contem os dados que queremos graficar tabela, seguido pelo argumento “col” que define as cores de acordo com as linhas da tabela, por sua vez definimos se a legenda será plotada com o argumento “legend.text” e por último indicamos a posição e o formato da legenda por meio do argumento “args.lengend”. Neste último argumento precisamos inserir a função list() na qual indicamos a posição da legenda pelo argumento “x”, o argumento “bty” o qual define que a legenda não tera uma caixa desenhada no seu entorno e o argumento “inset” que define a posição da legenda em relação ao eixo x.

3.3 Considerações

Durante nosso percurso neste capítulo realizamos etapas que consistem na construção dos dados no próprio programa do R e a condução da análise do qui-quadrado para ajuste das frequências e para a independência. A construção dos dados tem como resultado final um objeto similar a planilha de dados que deve ser importada, caso já a tenha preparado, e juntamente com a sumarização dos dados temos as mesmas etapas trabalhadas no capítulo anterior. A partir daí temos a condução da análise estatística pelo qui-quadrado. Um resumo gráfico das etapas pode ser observado aqui (Figura 3.2).

Resumo dos passos abordados no capítulo: da preparação dos dados até a análise dos dados.

Figura 3.2: Resumo dos passos abordados no capítulo: da preparação dos dados até a análise dos dados.

3.4 Exercícios

  1. Durante um longo período de observação sobre a trafego de carros na praia um pesquisador percebeu que durante a tarde o número de carros circulando era maior que durante a manhã. Ele resolveu tomar nota da quantidade de carros que passava em um determinado trecho da praia, durante vários dias, em ambos os períodos (manhã e tarde) e registrou, no total, os seguintes valores: 550 carros durante a manhã 620 carros durante a tarde. Considerando a observação do pesquisador e os valores por ele tomados, podemos corroborar ou refutar sua observação? Desenvolva a análise do qui-quadrado.

  2. Ao registrar o número de carros o pesquisador também registrou os dias da semana em que foram feitas as observações e obteve os seguintes valores:
  • Manhã de Quarta-feira: 130
  • Manhã de Sexta-feira: 420
  • Tarde de Quarta-feira: 178
  • Tarde de Sexta-feira: 442 A partir desses registros podemos dizer que o número de carros por período do dia (manhã e tarde) é independente do dia da semana (Quarta-feira e Sexta-feira)?

  1. Considerando os dados do exercício anterior. Obtenha a tabela com os dados em percentuais do número de carros por período do dia em relação aos dias da semana.

  2. Defina erro do tipo 1 e erro do tipo 2. Considerando o exercício 2. Qual dos erros (tipo 1 ou tipo 2) é assumido a um nível de confiança de 95%?

  3. Plote um gráfico com a tabela obtida no exercício 3.

  1. Vetores é uma estrutura básica do R que consiste em um objeto que contêm elementos de mesma classe. Se realizarmos o comando c(1, 2, 3), criamos um vetor, mas não um objeto. Se criarmos o seguinte: teste <- c(1, 2, 3) estaremos criando um objeto do tipo vetor.↩

  2. É um conjunto de elementos com estrutura n-dimensional, ou seja, com várias linhas e colunas, onde todos os seus elementos são de mesmo tipo (númerico, inteiro, fator, caracter etc).↩

  3. Zar, J. H. (2010). Biostatistical analysis (5th ed.). Upper Saddle River, N.J.: Prentice-Hall/Pearson.↩