Capítulo 2 Importar, organizar e sumarizar os dados

2.1 1° passo: Definir o ambiente de trabalho e importar a planilha de dados para o R

Ao se trabalhar com R a primeira pergunta que nos vem à cabeça é: Como inserir meus dados neste ambiente de trabalho? A resposta é simples e também complexa, pois depende do formato do arquivo de dados que está usando ( *.csv, *.xls, *.xlsx, *.txt entre outros). Para um mesmo formato existem inúmeras comandos possíveis para importar os dados. Não iremos especificar todas os comandos, mas os mais comuns (*.csv e *.xlsx), utilizando os comandos básicos do R e também por meio da interface gráfica do RStudio.

Para importar a planilha é necessário definir o ambiente de trabalho no seu computador. Este ambiente é a pasta de seu computador onde sua planilha e seus demais dados a serem trabalhados se encontram. Podemos realizar isso via linhas de comando ou pela própria interface do RStudio. Se realizado por linhas de comandos há diferença entre o sistema operacional (Windows, Linux ou macOS) que estiver utilizando. Aqui estaremos trabalhando com o sistema operacional Windows.

2.1.1 Definindo ambiente de trabalho via linha de comando

Para o sistema operacional Windows utilizamos o seguinte comando: setwd(choose.dir(path)), onde path é o caminho do diretório escolhido.

Se no Windows utilizarmos apenas a linha de comando setwd(choose.dir()) sem especificar o caminho a seguinte janela irá aparecer (Figura 2.1), a partir da qual iremos selecionar a pasta onde estão os arquivos que iremos trabalhar e salvar nosso script.

Figura 2.1: Janela que será aberta ao executar o comando: setwd(choose.dir()), no sistema operacional Windows.

A função setwd() é responsável por selecionar o diretório a ser trabalhado. Após isso podemos importar a planilha com os dados que utilizaremos.

Como resultado desta etapa podemos verificar a guia Files⁷, nela agora situa-se as pastas e arquivos da pasta que selecionamos e onde estará salvo nosso script quando o salvarmos.

2.1.2 Definindo ambiente de trabalho via interface gráfica

Diversas formas podem ser utilizadas para definir o ambiente de trabalho, apresentaremos 3. A primeira consiste em usar o atalho do teclado $(CTRL + SHIFT + H)$ e nela selecionaremos o ambiente de trabalho; a segunda via consiste em acessar a guia Session ir até a opção Set Working Directory e selecionar a opção Choose Directory da mesma forma que a opção anterior a mesma janela irá aparecer; por último podemos usar a guia Files onde podemos clicar nos 3 pontos “…” que aparecem no canto superior direito da guia e buscar o ambiente/pasta que iremos utilizar e a seguir na engrenagem (More) e selecionar a opção Set as Working Directory (Figura 2.2).

Figura 2.2: Guia Files indicando a opção para definir o local do computadors que será utilizado como ambiente de trabalho

2.1.3 Importando planilha via linha de comando:

Primeiro construa as planilhas a seguir nos formatos *.csv (usando vírgula como separador de colunas e ponto como separador decimal) (Figura 2.3) e *.xlsx (Figura 2.4) em um editor de planilhas, como excel, libreoffice calc ou outros e a salve com o nome de planilha.csv e planilha.xlsx no diretório que definiu previamente. A seguir demonstraremos as diferenças na importação de ambas as planilhas.

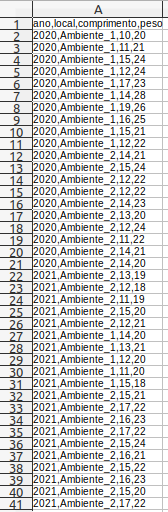
Planilha com os dados no formato *.csv que deve ser construída em algum editor de planilhas e salva na pasta de trabalho definida previamente

Figura 2.3: Planilha com os dados no formato *.csv que deve ser construída em algum editor de planilhas e salva na pasta de trabalho definida previamente

Planilha com os dados no formato *.xlsx que deve ser construída em algum editor de planilhas e salva na pasta de trabalho definida previamente

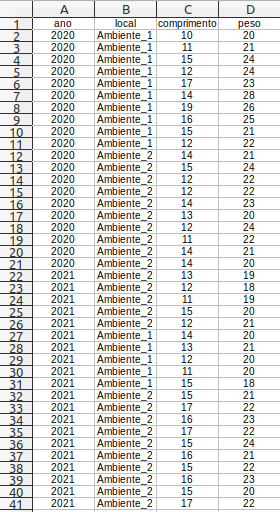
Figura 2.4: Planilha com os dados no formato *.xlsx que deve ser construída em algum editor de planilhas e salva na pasta de trabalho definida previamente

Digite em seu script a seguinte linha de comando:

dados <- read.csv(file = "planilha.csv", header = TRUE, sep = ",")

OBS: Não se esqueça de definir previamente o ambiente de trabalho e verificar que o arquivo planilha.csv encontra-se presente nele.

O comando read.csv() importou a planilha que está no formato *.csv utilizando os argumentos “file” o qual indica o nome do arquivo a ser importado; “header” o qual indica se as colunas da planilha tem nome e “sep” o qual indica qual o caracter separador das colunas.

OBS: repare que há o operador “<-” , esse é o operador de atribuição, ele indica que o elemento a sua direita (seja um valor ou uma função) será atribuído ao elemento que está a sua esquerda (geralmente um novo objeto). Neste caso o elemento retornado pela função read.csv(file = “planilha.csv”, header = TRUE, sep = “,”) será atribuído a um objeto chamado dados.

O comando acima importou a planilha e o guardou em um objeto chamado dados que será o que nós utilizaremos de agora em diante sempre que quisermos acessar essa planilha no RStudio.

Para importar arquivos que estão no formato *.xls ou *.xlsx é necessário a instalação de algum pacote⁸ que permita a realização desse processo. Um pacote que instalaremos aqui é o readxl.

install.packages("readxl")
library(readxl)

dados <- read_excel(path = "planilha.xlsx", col_names = TRUE)

Os comandos read.csv() e read_excel() são similares, embora seus argumentos sejam diferentes. O argumento “path” é similar ao “file”, o argumento “col_names” é similar ao “header”. Repare que não temos o argumento “sep”, pois em um arquivo excel as variáveis são salvas em colunas. Observe que independente da forma de importação (que é dependente do formato do arquivo *.csv ou *.xlsx) o resultado final é o mesmo (Figura 2.5).

Figura 2.5: Resultado da importação do arquivo observado na guia environment. Há um objeto de nome dados, com 40 observações e 4 variáveis.

2.1.4 Importando planilha via interface gráfica:

Para importar a planilha com os dados via interface do RStudio devemos acessar a guia Environment e nesta acessar a opção Import Dataset a seguir temos várias opções a qual devemos escolher referente a extensão do arquivo que vamos importar, no nosso caso será a opção From Excel (Figura 2.6).

Figura 2.6: Tópicos para importação ddos dados pela via grafica.

Neste momento uma janela irá abrir (Figura 2.7) e no canto superior direito haverá o nome Browse onde deveremos clicar e escolher o arquivo com o qual iremos trabalhar. Em Import options no canto inferior esquerdo haverá algumas opções, na opção name deveremos renomear para dados, para coincidir com as vias que fizemos anteriormente. As demais opções podemos deixar em branco. Repare que no canto inferior direito aparecerá um comando relativo ao processo de importação similar ao que fizemos no tópico anterior e, aparecerá também, um comando chamado View() que veremos mais adiante, para desabilita-lo basta desmarcar a caixa ao lado de mesmo nome. Conclua o processo clicando em import no canto inferior direito.

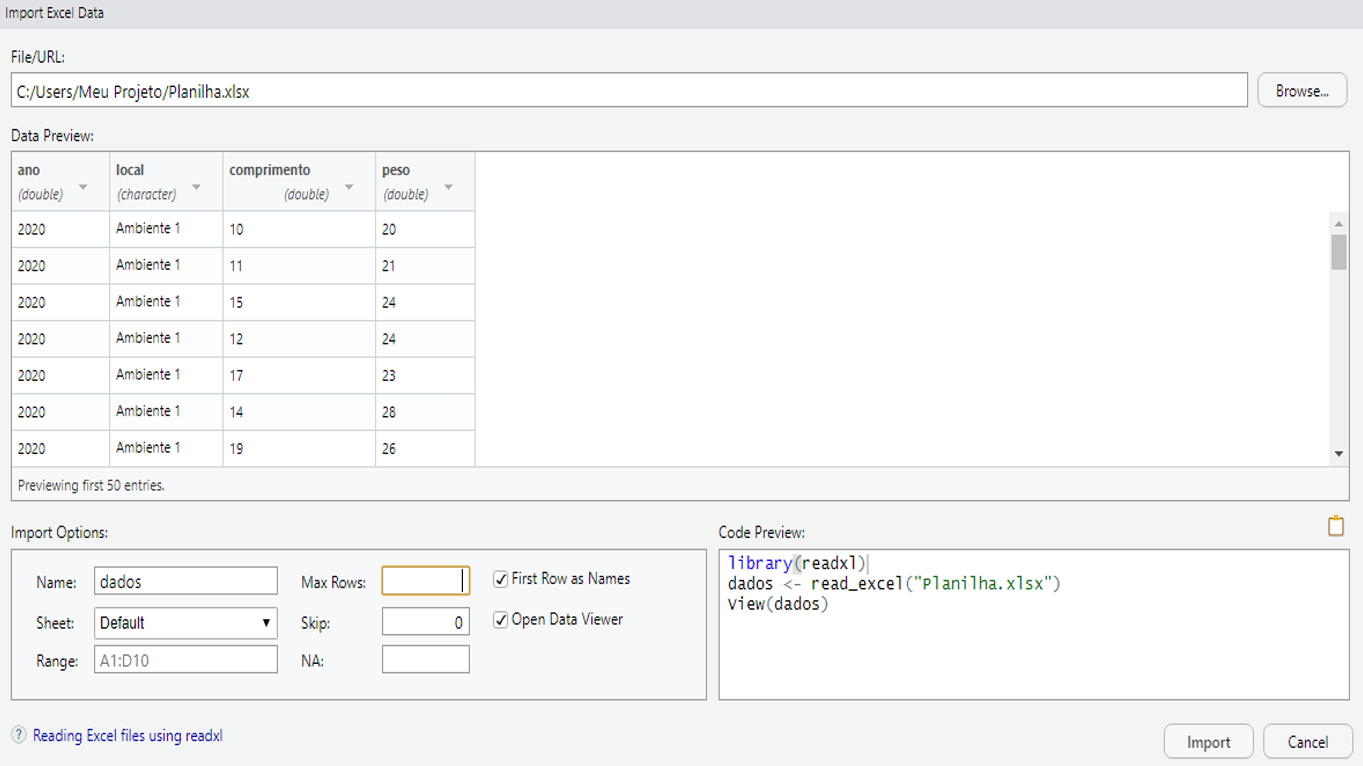
Figura 2.7: Importação dos dados pela via gráfica

2.2 2° passo: Verificar e ajustar os dados

Uma falha inicial comum é passar para as análises antes de verificar se os dados estão corretamente organizados, após a importação. Uma forma de previnir isso é conhecendo os seus dados e sabendo o que eles significam. Os dados, geralmente, podem ser: categóricos (ou qualitativos) ou mensuráveis (ou quantitativos). Quando categóricos temos de informar que eles consistem em fatores. Para isso vamos executar alguns comandos onde poderemos avaliar se no processo de importação as variáveis presentes na planilha de dados são reconhecidas como esperamos que seja.

Ao executarmos a função str() do arquivo dados podemos ver no console o seguinte resultado

str(dados)

## tibble[,4] [40 × 4] (S3: tbl_df/tbl/data.frame)
##  $ ano        : num [1:40] 2020 2020 2020 2020 2020 2020 2020 2020 2020 2020 ...
##  $ local      : chr [1:40] "Ambiente 1" "Ambiente 1" "Ambiente 1" "Ambiente 1" ...
##  $ comprimento: num [1:40] 10 11 15 12 17 14 19 16 15 12 ...
##  $ peso       : num [1:40] 20 21 24 24 23 28 26 25 21 22 ...

Seu resultado nos informa sobre o tipo de objeto que o arquivo é. Todo objeto pertence a alguma classe neste caso nosso objeto e da classe tibble ou data frame⁹.

Também nos é mostrado as variáveis presentes na planilha dados (ano, local, comprimento e peso), cada variável é, também, um objeto e portanto tem suas classes definidas automaticamente, o que pode ser visualizado ao lado de cada variável.

num = numeric (númerico), chr = character (caracter) e há outras que não estão indicadas aqui, como logic (lógica), integer (inteiro), factor (fator) entre outros.

Repare que a variável ano foi indicada como numérico. Variáveis consideradas numéricas são aquelas as quais foram mensuradas. Ano, embora númerica, não é uma variável possível de ser medida, porém devido ao seu registro ter sido em valores numéricos foi assim que ela foi entendida. Portanto temos que transforma-la.

Pensando no que definimos acima com variáveis categóricas e mensuráveis, ano e local podem ser classificados como variáveis categóricas. Devemos transformar em fator todas as variáveis de nossas planilha consideradas categóricas. Para isso utilizamos a função as.factor() a qual realiza esse processo que pode ser feito da seguinte forma:

dados$ano <- as.factor(dados$ano)
dados$local <- as.factor(dados$local)

Repare que nesses comandos inserimos o operador “$” (cifrão). Esse é um operador importante em toda linguagem de programação e será bastante utilizado. Ele permite acessar alguma variável dentro de um objeto. Pensando no objeto dados, ao colocarmos seu nome e em seguida o operador “$” podemos acessar as variáveis dentro dele.

O comando portanto é lido da seguinte forma:

dados$ano <-: indica que uma variável ano será criada dentro do objeto dados.
as.factor(dados$ano): indica que o objeto criado consistirá na variável ano que está no objeto dados porém considerando-a como factor.

Uma dúvida que pode aparecer aqui é: O que aconteceu com a variável ano que já existia dentro da planilha dados? Temos duas variáveis ano, agora?

A resposta é que quando criamos um objeto ou variável com o mesmo nome de um já existente o anterior é substituído. Conduza o seguinte exemplo.

Crie o objeto idade que contenha o valor de 30.

idade <- 30

Repare o objeto idade criado no environment.

Agora crie e execute um segundo objeto de mesmo nome, porém valor diferente, e repare no enviroment.

idade <- 40

Reparou que ao criar um segundo objeto de mesmo nome que antes o primeiro foi apagado e substituído pelo segundo? Este é o mesmo processo que ocorreu quando realizamos a função que definiu ano e local como fatores dentro do objeto dados.

Vamos observar novamente a função str() para verificar se ano e locais, agora, são fatores

str(dados)

## tibble[,4] [40 × 4] (S3: tbl_df/tbl/data.frame)
##  $ ano        : Factor w/ 2 levels "2020","2021": 1 1 1 1 1 1 1 1 1 1 ...
##  $ local      : Factor w/ 2 levels "Ambiente 1","Ambiente 2": 1 1 1 1 1 1 1 1 1 1 ...
##  $ comprimento: num [1:40] 10 11 15 12 17 14 19 16 15 12 ...
##  $ peso       : num [1:40] 20 21 24 24 23 28 26 25 21 22 ...

Como pode verificar agora temos 2 variáveis como fatores e 2 como numéricas. Mais que isso, essa função nos indica ao lado dos fatores um w/2 levels que está nos dizendo que essa variável tem 2 níveis. De maneira similar, as variáveis numéricas indicam colchetes com os seguintes valores [1:40] que significa que temos 40 valores/observações/linhas.

Observe a planilha dados no environment. Note que ao lado do nome dados há escrito 40obs. of 4 variables. Isto indica que temos 40 observações e 4 variáveis.

Que tal agora observarmos nossa planilha? Podemos fazer isso por meio da execução função head() do nosso objeto (dados). Onde no console são mostradas as primeiras linhas de nossa planilha

head(dados)

## # A tibble: 6 x 4
##   ano   local      comprimento  peso
##   <fct> <fct>            <dbl> <dbl>
## 1 2020  Ambiente 1          10    20
## 2 2020  Ambiente 1          11    21
## 3 2020  Ambiente 1          15    24
## 4 2020  Ambiente 1          12    24
## 5 2020  Ambiente 1          17    23
## 6 2020  Ambiente 1          14    28

Outra maneira é executarmos a função View() que abre uma aba, ao lado de seu script mostrando todos os dados.

View(dados)

Experimente agora escrever o nome do objeto dados e executar, o que aparece? Experimente, também, clicar no nome do objeto dados, presente no environment. O que você observou?

Se no primeiro caso você observou seu objeto aparecendo no console, parabéns você está indo no caminho certo. Se no segundo momento você observou que ao clicar sobre o nome dados ele executou a mesma coisa que a função View() você está indo maravilhosamente bem. Continue assim!

Isto não é tudo, mas sim o necessário para começarmos a sumarizar os dados de maneira eficiente.

Não se esqueça que antes de trabalharmos nossos dados temos que entender o que eles são e a que eles se referem. A análise de dados sem prévio conhecimento sobre o que eles significam pode levar a interpretações errôneas, caso as análises realizadas indiquem algum resultado, ou a muita dor de cabeça, se algum comando para uma análise não funcionar como esperado.

Portanto sigam os passos precisamente, não pule etapas e busque diversificar a fonte do seu conhecimento. Pois o R é uma linguagem que como demonstramos até o momento há muitas vias possíveis de escrita para um mesmo objetivo e diferentes autores podem escrever de formas diferentes.

2.3 3° passo: Sumarizar os dados graficamente

Já importamos nossa planilha e já a ajustamos. Que tal começarmos a ver a “mágica” acontecer e graficarmos nossos dados?

Muitos gráficos podem ser realizados, mas lembre-se que há toda uma lógica por trás disso.

Pensando nos gráficos mais comuns e úteis para nosso dia-a-dia e que nos permitem sumarizar nossos dados, temos os histogramas, gráficos de barras, de pontos, de linhas e os boxplots. Vamos então começar com esses e com o objetivo inicial de sumarizar nossos dados.

2.3.1 Histograma

O histograma nos permite verificar a distribuição da frequência dos nossos dados. Por exemplo, imagine uma amostra com diversos indivíduos de um dado grupo. Caso queiramos representar as frequências relativas das diferentes faixas de peso deste grupo, podemos usar o histograma.

A função hist() permite visualizar os valores da variável comprimento (Figura 2.8). Vejamos o exemplo abaixo.

hist(dados$comprimento)

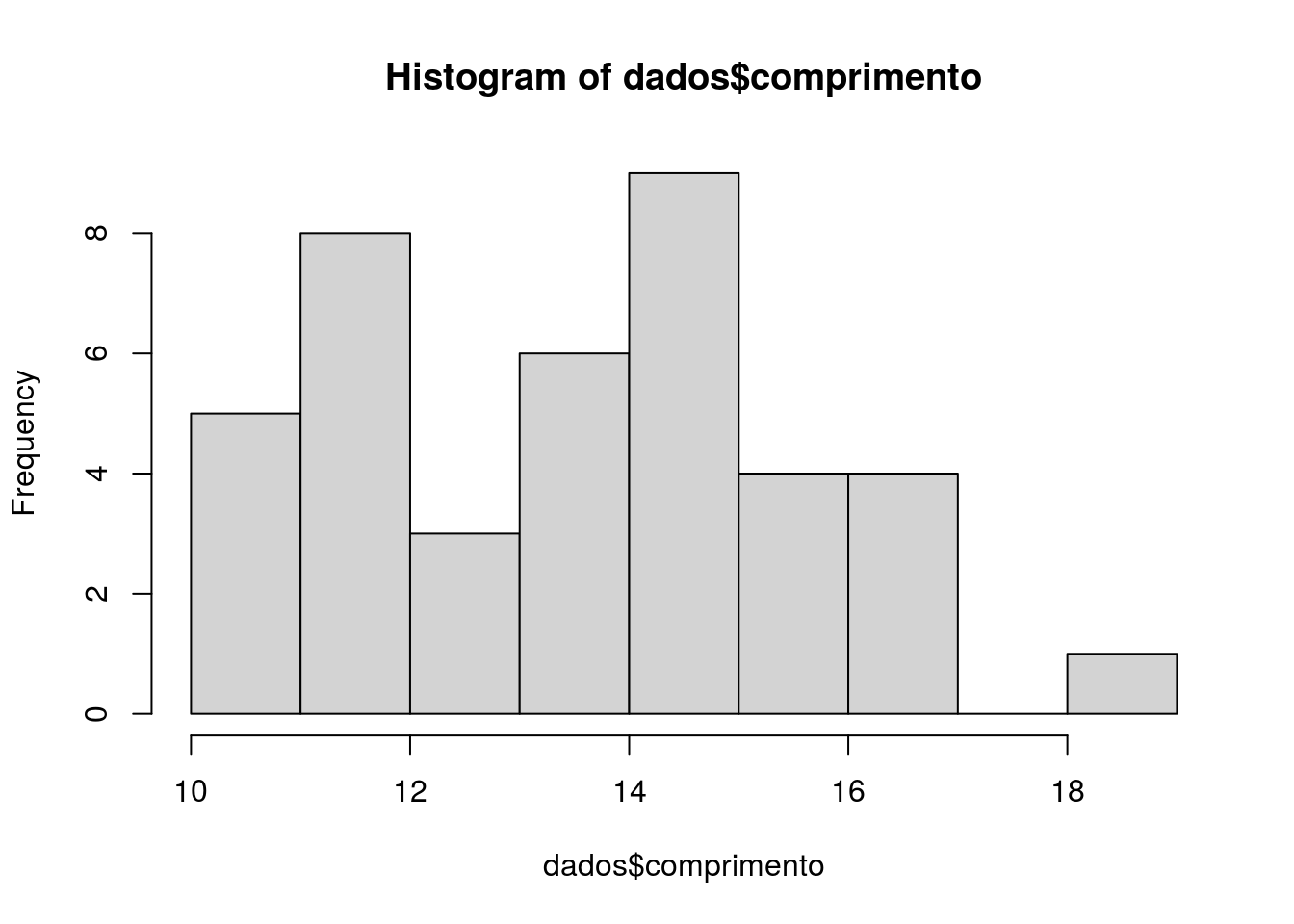
Figura 2.8: Comprimento dos organismos da planilha dados

Repare que um gráfico foi gerado na sua janela lateral, na guia plots.

Perceba também que voltamos a usar o operador “$” (cifrão).

Nosso gráfico não está com uma aparência muito agradável além de estar um pouco sem cor. Podemos editar e melhorar o aspecto do gráfico ao inserir cores ou outros argumentos estéticos que melhoram sua visualização e entender como ele sumariza nossos dados.

hist(dados$comprimento, 
     ylim = c(0, 10), 
     xlim = c(9, 20), 
     col = "blue",
     main = "Meu Histograma",
     xlab = "Comprimento",
     ylab = "Frequência absoluta")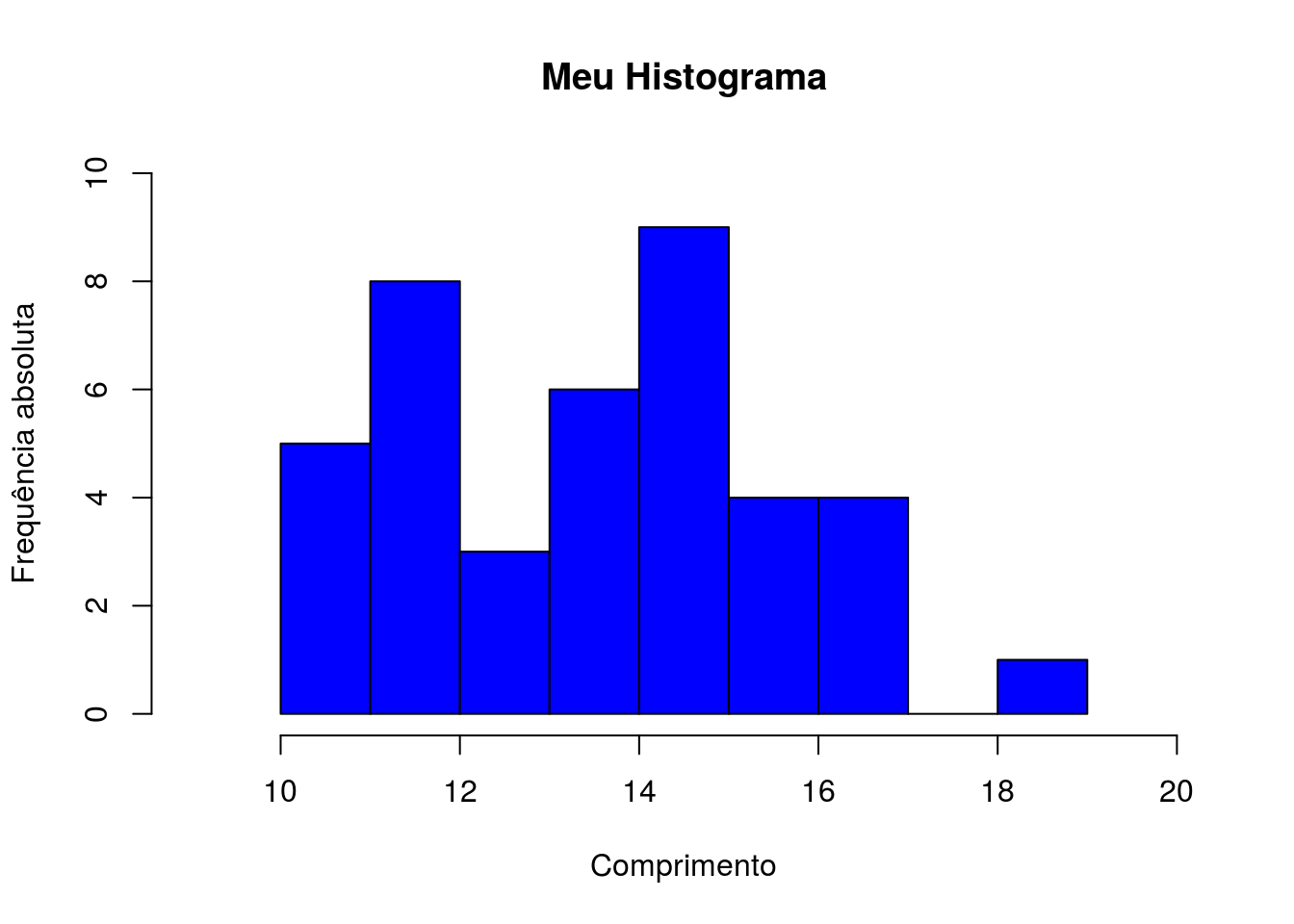

Figura 2.9: Comprimento dos organismos da planilha dados com barras coloridas

Temos aqui o histograma (Figura 2.9) com alguns argumentos que permitiram melhorar sua visualização. Agora é possível observar a variável comprimento e sua frequência de ocorrência.

Além disso podemos observar por meio desse que o valor mínimo observado é 10, que o máximo é 19 e que as frequências das diferentes classes de comprimento formadas variam entre 0 e aproximadamente 9. Será que isto que observamos está correto? Vamos ver no tópico a seguir (4° passo: Sumarizar os dados numericamente).

Ainda em relação ao histograma é possível ver na função hist() que utilizamos diversos argumentos como: “xlim”, “ylim”, “col”, “main”, “xlab” e “ylab”, além de uma função chamada c().

xlim: define os limites do eixo x;
ylim: define os limites do eixo y;
col: define as cores de preenchimento das barras;
xlab: define o nome do eixo x;
ylab: define o nome do eixo y;
c(): concatena (une) valores;

OBS: Essa função c() é muito importante e será utilizada constantemente ao longo de seu trajeto no R.

2.3.2 Gráfico de Barras

O gráfico de barras é um dos mais utilizados. Com ele podemos comparar valores de categorias diferentes. Por exemplo, dados onde temos números de indivíduos de diversas espécies podem ser representados em gráficos de barras, onde cada espécie será representada por uma barra.

Se já chegamos até esse ponto vamos exercitar um pouco antes de plotar o gráfico de barras. Construa a seguinte planilha no seu editor de planilhas (Figura 2.10) e nomeie-a de abundancia.

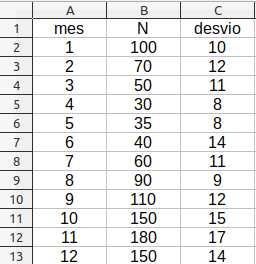
Figura 2.10: Planilha de dados de abundância.

Acesse a planilha abundância. Vamos inseri-la no R com o nome abundancia. repare que retirei o acento e as letras estão em minúsculo. Sempre que trabalharmos com linguagem de programação evite acentuações, espaços, cedilhas (ç) e atente a maiúsculas e minúsculas, pois isso pode interferir no seu código

OBS: Se estiver iniciando o R agora lembre-se de definir o ambiente de trabalho.

abundancia <- read_excel("abundancia.xlsx", col_names = TRUE)

Repare que ela está no formato *.xlsx e apresenta as seguintes variáveis: mes, N e desvio. Onde N significa o número de indivíduos observados e desvio o desvio padrão.

Vamos apenas conferir se está tudo certo com os dados usando a função str().

str(abundancia)

## tibble[,3] [12 × 3] (S3: tbl_df/tbl/data.frame)
##  $ mes   : num [1:12] 1 2 3 4 5 6 7 8 9 10 ...
##  $ N     : num [1:12] 100 70 50 30 35 40 60 90 110 150 ...
##  $ desvio: num [1:12] 10 12 11 8 8 14 11 9 12 15 ...

Vamos converter a variável mês em factor.

abundancia$mes <- as.factor(abundancia$mes)

Repare que agora que sabemos os passos a realizar, da importação dos arquivos até este momento tudo ficou muito mais fácil e fluido e apenas realizamos três etapas, sendo uma delas apenas para conferir os dados.

Seguimos então para o gráfico de barras (Figura 2.11), a fim de mostrar o número de indivíduos ao longo dos meses. Para isso utilizaremos a função barplot().

barplot(abundancia$N)

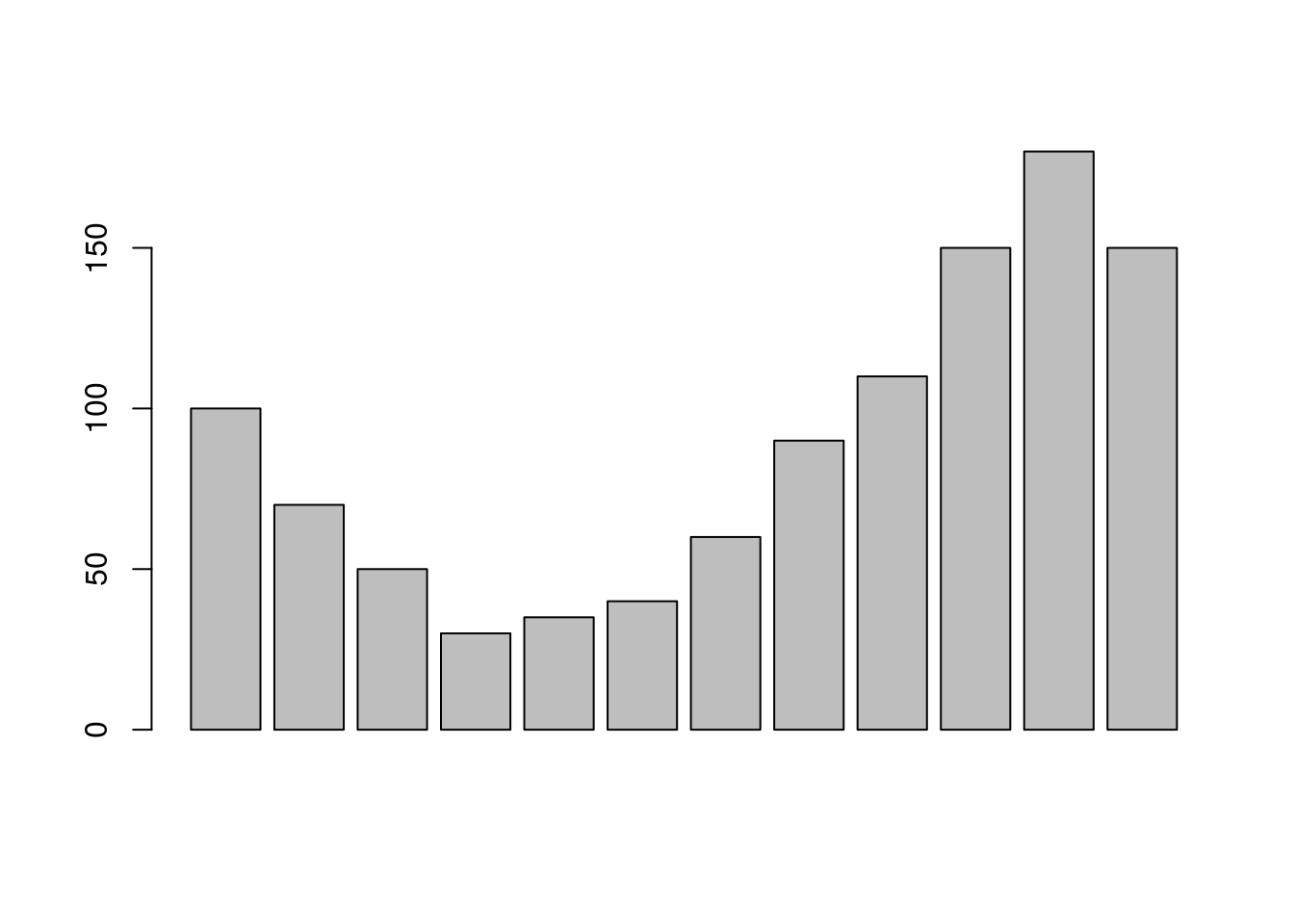
Figura 2.11: Gráfico de barras com número de indivíduos da planilha abundância por mês

Assim como o histograma, o simples uso da função sem argumentos gera um gráfico de difícil análise e esteticamente não muito agradável.

Vamos portanto adicionar alguns argumentos já conhecidos e outros novos que permitirão a melhor análise do gráfico (Figura 2.12).

barplot(abundancia$N,
        ylim = c(0, 200),
        xlab = "Mês",
        ylab = "Abundância",
        names.arg = abundancia$mes,
        col = "green")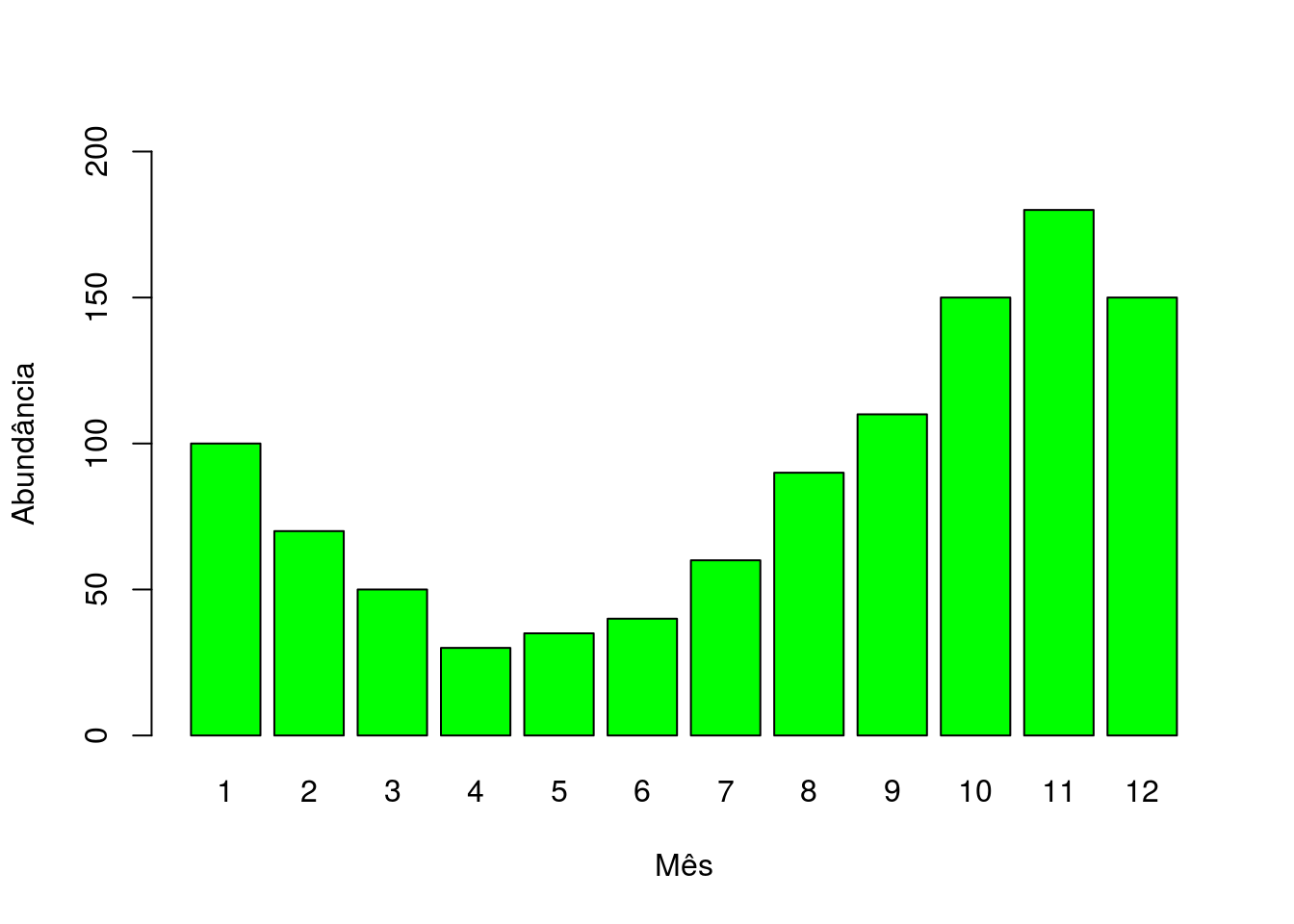

Figura 2.12: Gráfico de barras com número de indivíduos da planilha abundância por mês, com barras coloridas

No código acima definimos o que será graficado, como a variável N presente no objeto abundância e informamos isso por meio do operador “$” (cifrão). Ajustamos os limites do eixo “y” através do argumento “ylim” em 0 e 200, usando a função concatenar c(). Definimos os nomes dos eixos x e y por meio dos argumentos “xlab” e “ylab”, respectivamente. Definimos o nome das barras de acordo com a variável mes, também presente no objeto abundancia e por último definimos a cor das barras, usando o argumento “col”, como verde.

Podemos extrair desse gráfico que a abundância dos indivíduos variam ao longo dos meses com valores menores em torno de 50 indivíduos nos meses 4, 5 e 6 e valores maiores em torno de 200 indivíduos no mês 11.

2.3.3 Gráfico de Pontos e de Linhas

Quando queremos representar dados quantitativos em ambos os eixos, podemos usar tanto o gráfico de pontos quanto o de linhas. Com eles geralmente podemos verificar a relação entre as variáveis (gráfico de pontos) ou a tendência dos nossos dados em ordem cronológica (gráfico de linhas). Por exemplo, podemos representar num gráfico de linhas a variação da quantidade de indivíduos de uma espécie ao longo do ano ou os valores de precipitação ao longo de décadas.

Para fazer um gráfico seja de pontos ou de linhas pelo comando básico do R (utilizamos a função plot()) precisamos indicar que ambos os eixos apresentam variáveis numéricas. Portanto teremos que modificar a variável mês de fator para número. Porém não precisamos fazer isso em um comando separado podemos aplicar a função que converte uma variável em numérica dentro da função que plota o gráfico. Vamos visualizar como isso ocorre na prática (Figura 2.13).

plot(x = as.numeric(abundancia$mes), y = abundancia$N)

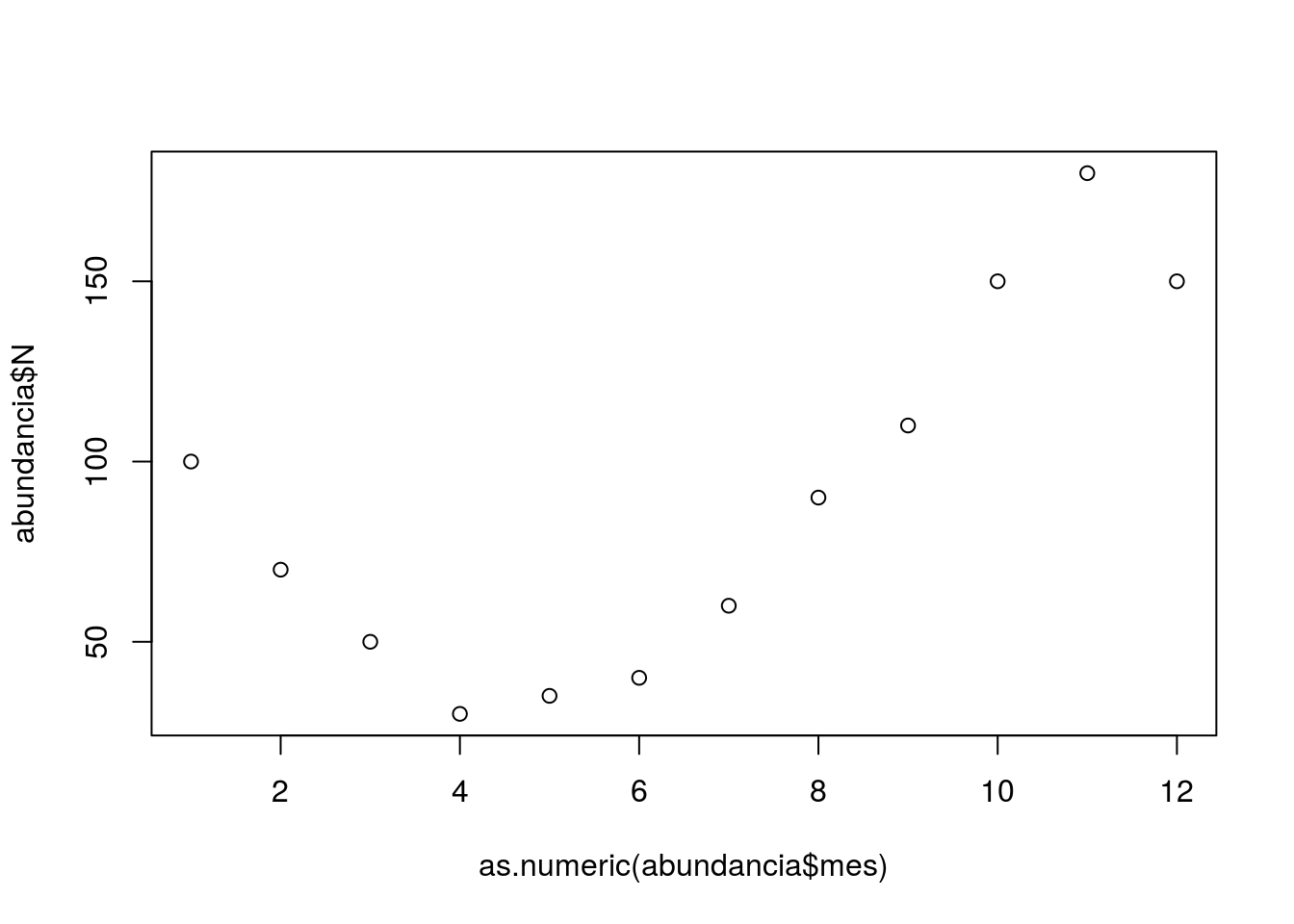
Figura 2.13: Representação gráfica do número de indivíduos por mês em pontos

Pronto, na função acima aplicamos a função plot() indicando os argumentos x e y que definem quem estará no eixo x e quem estará no eixo y, e para a variável que estará no eixo x (variável mês) adicionamos a função as.numeric(), a qual a converte em numérico apenas para a execução do plot.

Porém a função plot() não realizou um gráfico de linhas como esperado, pois para isso precisamos indica-lo por meio de argumentos. Como demonstraremos a seguir (Figura 2.14).

plot(x = as.numeric(abundancia$mes), 
     y = abundancia$N, 
     xlab = "Mês",
     ylab = "Abundância",
     main = "Meu gráfico de linha",
     ylim = c(0, 200),
     type = "l",
     col = "green",
     lwd = 2)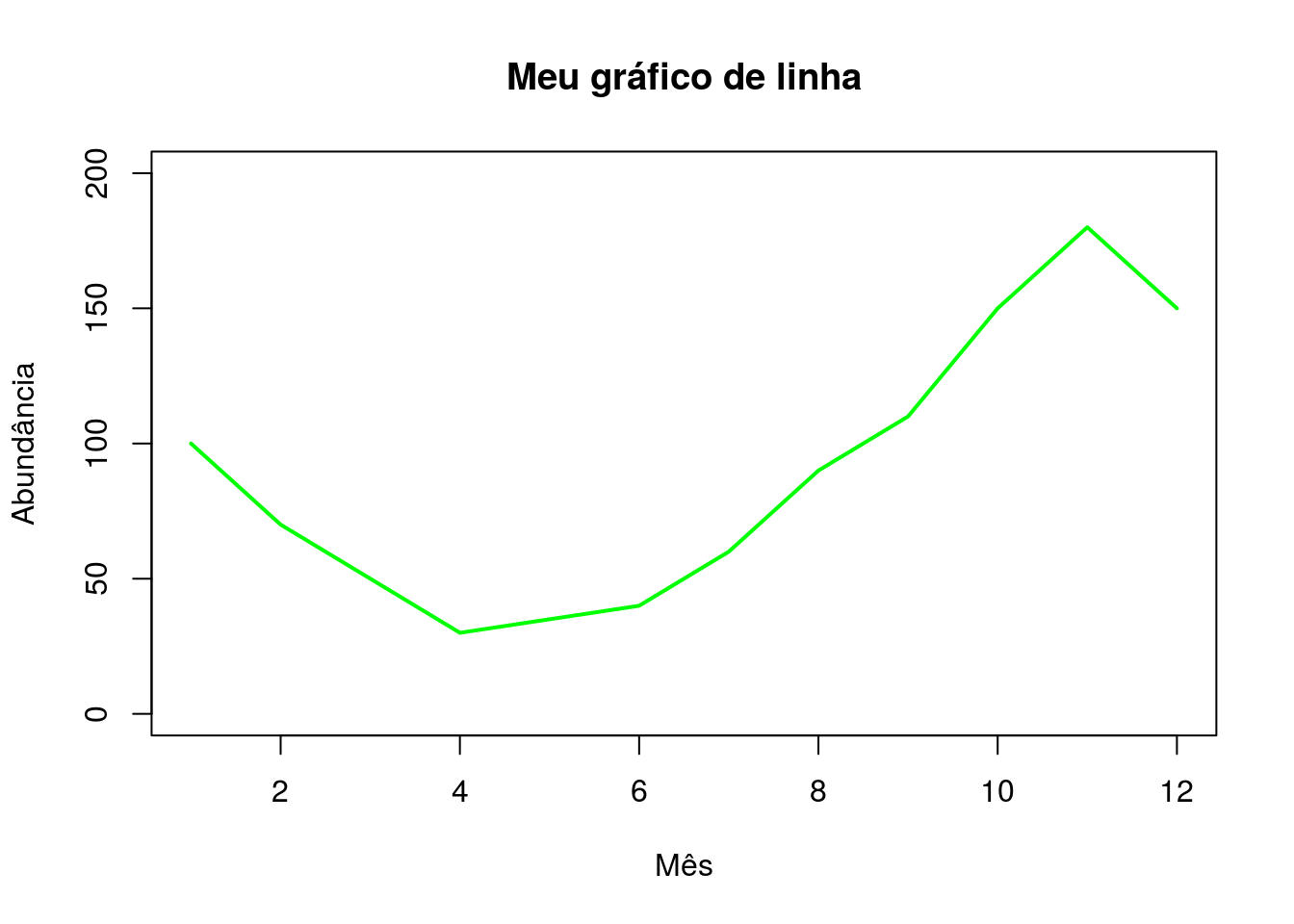

Figura 2.14: Representação gráfica do número de indivíduos por mês em um gráfico de linhas

Repare que inserimos alguns argumentos novos:

main: que insere o título do gráfico;
type: que define que será um gráfico de linhas;
lwd: que determina a espessura da linha;

2.3.4 Boxplot

Podemos usar os bloxplots para verificar a tendência das amostras e a distribuição destas. Quando se tem uma pequena quantidade de amostras (por exemplo, 3 réplicas) esse gráfico não é indicado. Nele também podemos verificar se temos alguma anomalia nos dados, os chamados outliers.

Vamos voltar a nossa primeira planilha dados e executar um gráfico do tipo boxplot (Figura 2.15) e ver o que ele nos informa. Para isso utilizaremos a função boxplot().

boxplot(formula = dados$comprimento ~ dados$ano)

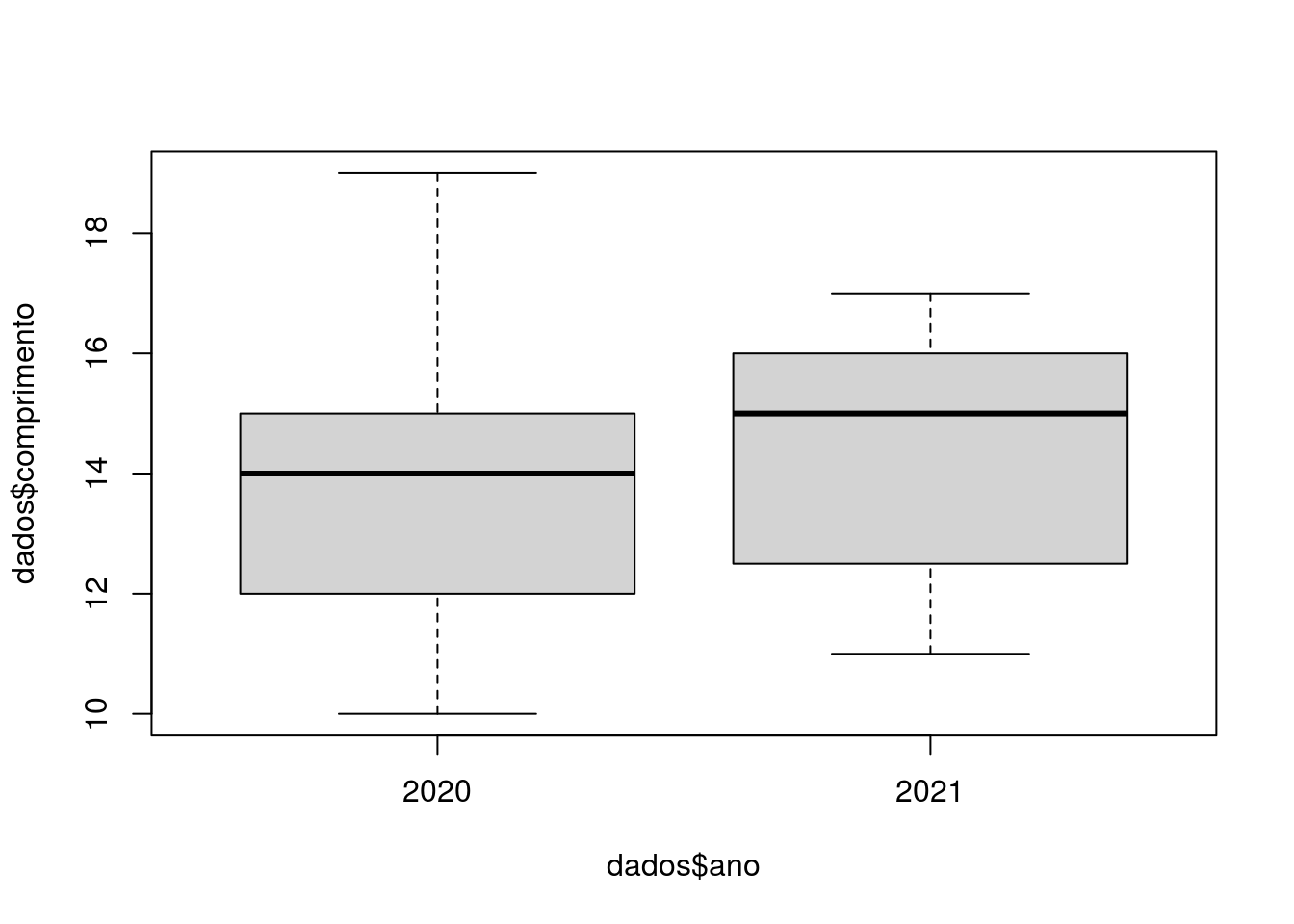
Figura 2.15: Gráfico tipo boxplot do comprimento por ano, da planilha dados

Repare que a escrita para esse gráfico é ligeiramente diferente. Dentro desta função há um argumento chamado “fórmula”, onde inserimos a variável independente (variável do eixo X) e a variável dependente (variável do eixo Y). Entre ambas as variáveis há o caracter “~” (til). A forma de ler essa escrita é a seguinte: Realize um boxplot da variável comprimento do objeto dados em função da variável ano do objeto dados. O caracter til é lido como (“em função de”)

Vamos adicionar alguns argumentos que permitem deixar o gráfico mais apresentável (Figura 2.16).

boxplot(formula = dados$comprimento ~ dados$ano,
        col = c("blue", "green"),
        xlab = "Ano",
        ylab = "Comprimento",
        main = "Meu Boxplot")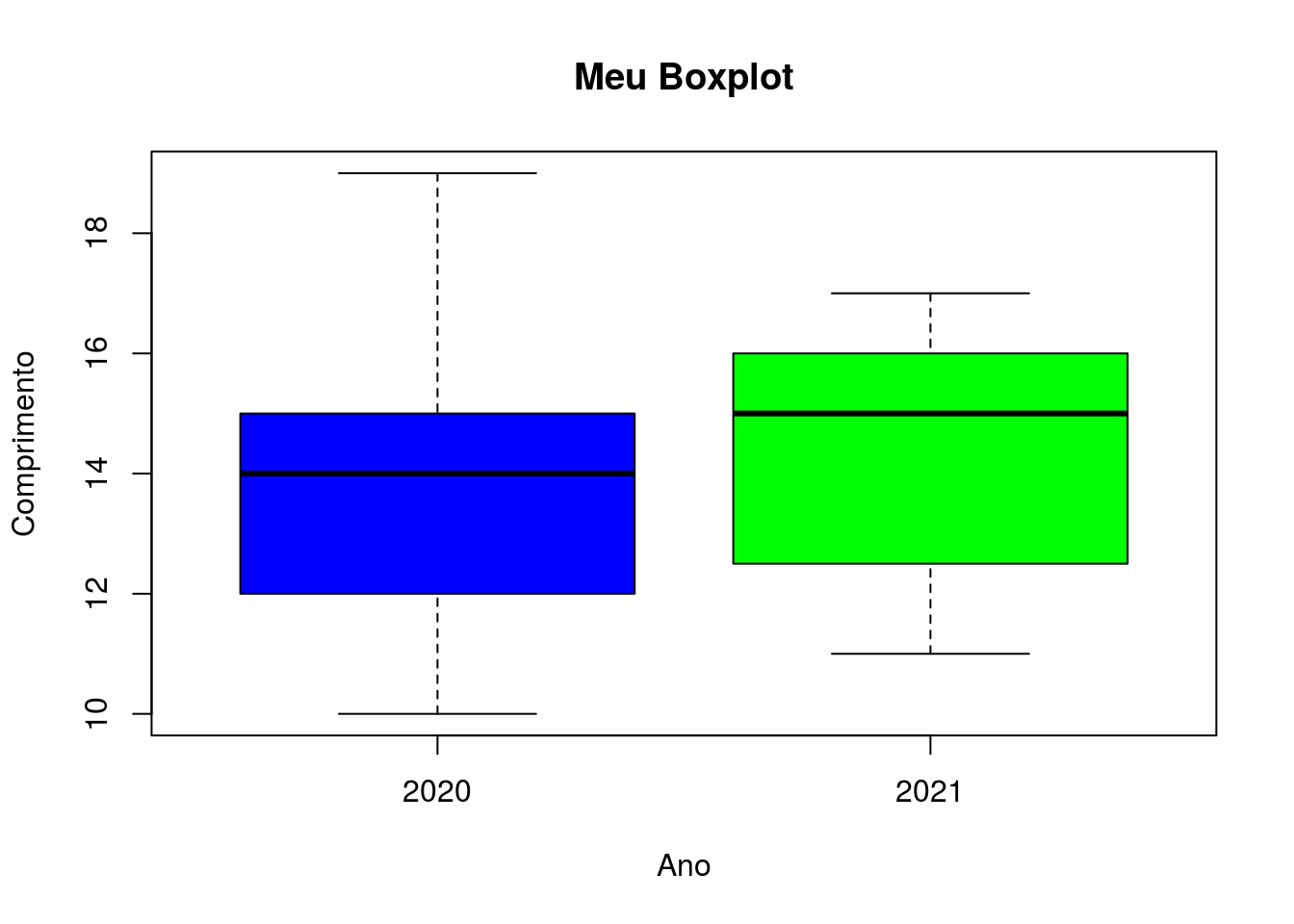

Figura 2.16: Gráfico tipo boxplot do comprimento por ano com cores por ano, da planilha dados

Repare que não adicionamos nenhum argumento ou função diferente do que já fizemos anteriormente. Ou seja, uma vez conhecendo a função, os argumentos por vezes se repetem entre funções com o mesmo objetivo (neste caso o objetivo é gerar um gráfico).

O boxplot porém nos fornece algumas informações extras em relação ao resumo dos dados. Podemos extrair dele dados como média, mediana (segundo quartil), primeiro e terceiro quartil, assim como máximos e mínimos da variável dependente (variável do eixo y).

As linhas de cada box (caixa) que se referem a cada um dos anos representam, em suas extremidades, os valores máximos e mínimos de comprimento de cada ano. A base e o topo de cada box indicam o primeiro e terceiro quartil, respectivamente, do comprimento do referido ano. A linha no interior da caixa indica a mediana (segundo quartil) e a metade do box (não marcada graficamente) indica a média.

Podemos por meio desse gráfico, então, ter uma ideia do que os dados indicam quanto as medidas de tendência central e algumas medidas de dispersão em relação as categorias presentes.

2.4 4° passo: Sumarizar os dados numericamente

Temos visto, até este ponto, como resumir os dados graficamente, de maeira geral.

Porém muitas vezes precisamos demonstrar, numericamente, quais são os valores que resumem os nosso dados. Estes valores consistem nas medidas de tendência central e nas suas medidas de dispersão.

O R permite, de maneira simples, sumarizar os dados por meio da função summary().

summary(dados)

##    ano            local     comprimento         peso      
##  2020:20   Ambiente 1:15   Min.   :10.00   Min.   :18.00  
##  2021:20   Ambiente 2:25   1st Qu.:12.00   1st Qu.:20.00  
##                            Median :14.00   Median :21.50  
##                            Mean   :13.97   Mean   :21.73  
##                            3rd Qu.:15.00   3rd Qu.:23.00  
##                            Max.   :19.00   Max.   :28.00

summary(abundancia)

##       mes          N              desvio     
##  1      :1   Min.   : 30.00   Min.   : 8.00  
##  2      :1   1st Qu.: 47.50   1st Qu.: 9.75  
##  3      :1   Median : 80.00   Median :11.50  
##  4      :1   Mean   : 88.75   Mean   :11.75  
##  5      :1   3rd Qu.:120.00   3rd Qu.:14.00  
##  6      :1   Max.   :180.00   Max.   :17.00  
##  (Other):6

Repare que ao aplicarmos esta função o R nos informou as variáveis presentes nestas planilhas e quando fator indicou quais são e quantos de cada existem. Quando númerico, nos retornou valores como média, mediana (segundo quartil), mínimo, máximo, primeiro e terceiro quartis.

As medidas de tendência central mais conhecidas e aplicadas são média, mediana e moda.

Para obtenção da média precisamos somar todos os valores e dividir pela quantidade de valores ou, no R, podemos fazer isso de maneira mais simples por meio da função mean():

mean(dados$comprimento)

## [1] 13.975

Como podemos verificar a média do comprimento na planilha dados é de 13,975¹⁰.

De maneira similar podemos calcular a mediana, que consiste no valor central da distribuição de valores de uma dada variável. Podemos visualiza-la por meio da função median().

median(dados$comprimento)

## [1] 14

Percebe-se que o valor que se encontra no meio da distribuição da variável comprimento é 14.

Até o momento aprendemos a explorar e sumarizar nossos dados graficamente. Visualizamos também a função summary() aplicada aos dados, que nos indica as medidas de tendência central média e mediana assim como outras características das variáveis como os quartis, mínimo e máximo. Essas medidas apresentadas tem como função indicar as características gerais das variáveis com as quais você está trabalhando. Porém há outras medidas que explicam os dados que são constantemente requeridas.

Medidas de dispersão indicam a propagação dos dados em torno do valor central, ou seja, são utilizadas para demonstrar a variabilidade dos dados. Quando as medidas se concentrarem em torno do centro de distribuição dos dados (baixa dispersão), quer dizer que possuem baixa variabilidade. Quando os dados apresentam uma distribuição mais ampla em torno do seu valor central (alta dispersão), significa que apresentam uma alta variabilidade.

Os limites inferior e superior de uma dada variável quantitativa são denominados mínimo e máximo e podem ser obtidos por meio das funções que calculam o mínimo e máximo. Apesar de seu resultado aparecer na função summary(), que aplicamos anteriormente, podemos obtê-la separadamente para uma variável especifica. Para isso aplicamos as funções min() e/ou max().

min(dados$comprimento)

## [1] 10

max(dados$comprimento)

## [1] 19

Uma outra forma de obter os valores máximo e mínimo é usando a função range().

range(dados$comprimento)

## [1] 10 19

Novamente repare que usamos o operador cifrão ($) após o nome do conjunto de dados. Como você aprendeu anteriormente ele permite acessar as variáveis que estão dentro do objeto dados.

Com os valores mínimo e máximo podemos obter nossa primeira medida de dispersão dos dados. A amplitude que consiste na diferença entre seus valores. Esta é a forma mais simples de verificar a dispersão de seus dados. A vantagem dela é fornecer a distância na qual seus dados variam mantendo-se a mesma unidade de medida.

A amplitude é utilizada para dados quantitativos, descrever a variabilidade de uma amostra, porém não para inferência estatística. Podemos calcula-la simplesmente utilizando a substração das funções que nos retornam seus valores. Veja o exemplo abaixo.

max(dados$comprimento) - min(dados$comprimento)

## [1] 9

Uma outra forma de realizar esta mesma operação é utilizando a função diff() que calcula a diferença. Quando inserimos a função range() dentro da função diff() o R nos retorna o resultado da diferença dos valores obtidos pela função range(). Veja o exemplo abaixo.

diff(range(dados$comprimento))

## [1] 9

O desvio padrão é uma das medidas de variação mais importantes que iremos realizar. Ele mede a distância dos valores observados em relação a sua média.

Durante a coleta de dados em estudos ambientais, o que normalmente é extraído de informação é uma fração de um todo, por exemplo, uma amostra de uma população. Portanto quando se deseja avaliar o desvio padrão, assim como outras medidas de variabilidade, devemos considerar se estamos avaliando uma amostra ou toda a população. Se uma amostra é considerada, nos referimos a ela como desvio padrão amostral e a representamos por (s) se toda a população é considerada nos referimos a ela como desvio padrão populacional e a representamos por ($\sigma$).

Neste livro vamos abordar e considerar o desvio padrão amostral.

Para calcular o desvio padrão utilizamos a seguinte fórmula:

\[s = \sqrt{\sum^{N}_{i = 1}\frac{(x_{i}-\overline{x})²}{N-1}}\]

Onde, $\sum^{N}_{i=1}$ indica o somatório da expressão $\frac{(x_{i}-\overline{x})²}{N-1}$ para $i$ variando de 1 até o número total de elementos $N$. $x_{i}$ indica o valor medido da variável $x$, $\overline{x}$ indica a média da variável $x$ e $N$ indica o número total de elementos da variável $x$.

Podemos calcular o desvio padrão a partir de suas partes, considerando sua fórmula ou a partir de uma função pré-existente no R. Vamos conferir as duas formas.

Para facilitar o entendimento do código vamos começar criando os seguintes objetos: comp, com.media e N.

comp <- dados$comprimento
comp.media <- mean(dados$comprimento)
N <- length(dados$comprimento)

comp

##  [1] 10 11 15 12 17 14 19 16 15 12 14 15 12 12 14 13 12 11 14 14 13 12 11 15 12
## [26] 14 13 12 11 15 15 17 16 17 15 16 15 16 15 17

comp.media

## [1] 13.975

## [1] 40

comp: contêm os dados da variável comprimento presente na planilha dados
comp.media: contêm um dado que consiste na média da variável comprimento
N: representa a quantidade de observações presentes na variável comprimento. Repare que aqui utilizamos uma nova função chamada length() a qual contabiliza o número de observações de objeto.

Agora vamos realizar o desvio padrão de 3 formass. Onde na primeira vamos entender como lemos uma função. O ideal é ler de dentro para fora. Como uma equação matemática. Mas não se assuste é mais fácil do que parece. Nas outras 2 maneiras vamos aplicar uma função pre-existente no R.

sqrt((sum((comp - comp.media)^2)) / (N - 1))

## [1] 2.106005

sd(dados$comprimento)

## [1] 2.106005

sd(comp)

## [1] 2.106005

A leitura da primeira dá-se da seguinte forma:

(comp - comp.media): Realize a diferença dos valores presentes em comp de sua média.
((comp - comp.media)^2): Eleve esses valores, obtidos da diferença, ao quadrado.
(sum((comp - comp.media)^2)): Some todos os valores, obtidos pela diferença elevados ao quadrado.
(sum((comp - comp.media)^2)) / (N - 1): Divide a soma dos valores da diferença elevado ao quadrado pelo número de observações menos 1.
sqrt((sum((comp - comp.media)^2)) / (N - 1)): Extraia a raíz quadrada da divisão da soma dos valores da diferença elevado ao quadrado pelo número de observações menos 1.

Repare que a leitura segue a ordem dos passos do cálculo que seria feito a mão usando a equação apresentada acima.

Mas caso não queira escrever a fórmula, o R nos fornece a função sd() que pode ser aplicada a uma variável dentro de uma planilha de dados (segunda forma apresentada) ou a um vetor que contenha um conjunto de observações do seu interesse (terceira forma apresentada).

Pronto, agora entendemos como ler um código que apresenta funções dentro de funções e entendemos como realizar o desvio padrão de três formas distintas (existem diversas outras formas) no R. Agora você já pode escolher a que mais lhe agrada. Qual você prefere? Bem, essa é uma escolha sua.

Assim como o desvio padrão temos também a variância. Na variância, calculamos o grau de dispersão dos nossos dados em relação à média desses dados. Há todo um conjunto especial de análise de dados voltado para ela. Mas como poderão ver, ela não difere muito do desvio padrão, apenas pelo fato de que consiste no seu valor elevado ao quadrado, daí a variância amostral ser representada por s² enquanto que o desvio padrão é representado por s.

Partindo dessa ideia, a variância consiste em estimar o desvio padrão e eleva-lo ao quadrado (ou removermos a raíz quadrada da fórmula do desvio padrão). Vamos observar o seu resultado utilizando sua fórmula e a função predefinida pelo R.

(sum((comp - comp.media)^2)) / (N - 1)

## [1] 4.435256

sd(dados$comprimento)^2

## [1] 4.435256

var(dados$comprimento)

## [1] 4.435256

Pronto, aqui estão 3 formas de encontrar a variância de seus dados. A primeira é similar ao que realizamos anteriormente para o desvio padrão, porém sem a raíz quadrada. A segunda consiste em elevar ao quadrado o resultado do desvio padrão e a terceira é aplicando a função var() à variável comprimento presente na planilha dados.

Difícil? Espero que não.

O coeficiente de variação é outra medida importante e de fácil interpretação sobre a variabilidade dos dados. Este consiste em representar a variação em torno da média em termos percentuais. Este é simples de calcular e intuitivo de interpretar.

Não há, até o momento, uma função no pacote básico do R que o calcule. Vamos calcula-lo a partir de sua fórmula matemática e ver o que ele quer dizer.

sd(dados$comprimento)/mean(dados$comprimento)*100

## [1] 15.0698

Pronto, calculamos o coeficiente de variação da variável comprimento e obtivemos uma variação em torno da média de ±15,07%.

Com isso verificamos as principais medidas de tendência central e dispersão. Mas fica, aqui, uma questão. Como incorpora-las aos gráficos para que assim possamos resumir os dados graficamente de maneira mais completa?

Vamos utilizar nossa planilha dados e verificar a média do comprimento e do peso por ano e por ambiente e incorporar em cada um dos gráficos seus respectivos desvios padrões.

Neste caso vamos primeiro precisar organizar os dados que queremos plotar. Como desejamos plotar a média do comprimento por ano e ambiente com seus respectivos desvios padrões, vamos primeiro construir passo a passo uma tabela que apresente 4 colunas. A primeira com o ano, a segunda com ambiente, a terceira com a média do comprimento e a última com o desvio padrão.

Para isso vamos utilizar a função split(), que fragmenta um data frame em função de algum fator. Neste primeiro momento, vamos fragmentar o objeto dados em função do ano e alocar esses dois novos conjuntos de dados em um novo objeto chamado dados.2. Posteriormente vamos criar um objeto chamado ano.2020 onde vamos alocar o primeiro objeto (referente ao ano de 2020) que está dentro de dados.2 e um segundo objeto chamado ano.2021 onde vamos alocar o segundo objeto (referente ao ano de 2021) que está dentro de dados.2. Veja os comandos abaixo.

dados.2 <- split(x = dados, f = dados$ano)
ano.2020 <- dados.2$`2020`
ano.2021 <- dados.2$`2021`

Repare que foram criados no environment três novos objetos: dados.2 o qual consiste em um objeto da classe lista que contêm o objeto dados separado por ano; ano.2020 que consiste no objeto da classe data frame (mesma classe do objeto dados) que contêm as informações referentes, somente ao ano de 2020; e o objeto ano.2021, similar ao anterior, porém com as informações referentes ao ano de 2021.

A seguir vamos aplicar o mesmo racíocinio lógico para fragmentar os objetos ano.2020 e ano.2021 por locais.

ano.2020.local <- split(x = ano.2020, f = ano.2020$local)
ano.2021.local <- split(x = ano.2021, f = ano.2021$local)
ano.2020.local.1 <- ano.2020.local$`Ambiente 1`
ano.2020.local.2 <- ano.2020.local$`Ambiente 2`
ano.2021.local.1 <- ano.2021.local$`Ambiente 1`
ano.2021.local.2 <- ano.2021.local$`Ambiente 2`

Pronto! Dividimos nossos dados de acordo com os fatores que desejamos (ano e local) utilizando o argumento “f” da função split(). Agora vamos obter as métricas média e desvio padrão para cada ano de cada local. Para isso vamos criar novos objetos que alocam esses dados.

ano.2020.local.1.comp.media <- mean(ano.2020.local.1$comprimento)
ano.2020.local.1.comp.dp <- sd(ano.2020.local.1$comprimento)
ano.2020.local.2.comp.media <- mean(ano.2020.local.2$comprimento)
ano.2020.local.2.comp.dp <- sd(ano.2020.local.2$comprimento)
ano.2021.local.1.comp.media <- mean(ano.2021.local.1$comprimento)
ano.2021.local.1.comp.dp <- sd(ano.2021.local.1$comprimento)
ano.2021.local.2.comp.media <- mean(ano.2021.local.2$comprimento)
ano.2021.local.2.comp.dp <- sd(ano.2021.local.2$comprimento)

Pronto! Média e desvio padrão do comprimento calculado para cada ano e local e alocados em seus respectivos objetos. Agora vamos unir esses resultados, por meio da função c() em um objeto com os dados referentes a média dados.media e um outro com o desvio padrão dados.dp.

dados.media <- c(ano.2020.local.1.comp.media,
                 ano.2020.local.2.comp.media,
                 ano.2021.local.1.comp.media,
                 ano.2021.local.2.comp.media)
dados.dp <- c(ano.2020.local.1.comp.dp,
              ano.2020.local.2.comp.dp,
              ano.2021.local.1.comp.dp,
              ano.2021.local.2.comp.dp)

Agora, vamos criar as variáveis categóricas ano e local para adicionar aos dados de médias e desvios e unir esses objetos em um data frame chamado dados.3. Posteriormente vamos conferir as classes das variáveis.

Para isso durante este processo utilizaremos duas funções que não haviamos utilizado antes. As funções as.data.frame() que faz com que um conjunto de objetos sejam convertidos em data frame e cbind() o qual une objetos como colunas. Essas funções também serão comumente utilizadas durante seus passos iniciais no R.

ano <- c("2020", "2020", "2021", "2021")
local <- c("Ambiente 1", "Ambiente 2", "Ambiente 1", "Ambiente 2")
dados.3 <- as.data.frame(cbind(ano, local, dados.media, dados.dp))
str(dados.3)

## 'data.frame':    4 obs. of  4 variables:
##  $ ano        : chr  "2020" "2020" "2021" "2021"
##  $ local      : chr  "Ambiente 1" "Ambiente 2" "Ambiente 1" "Ambiente 2"
##  $ dados.media: chr  "14.1" "13.1" "13" "14.8"
##  $ dados.dp   : chr  "2.84604989415154" "1.28668393770792" "1.58113883008419" "1.93464651625488"

dados.3$ano <- as.factor(dados.3$ano)
dados.3$local <- as.factor(dados.3$local)
dados.3$dados.media <- as.numeric(dados.3$dados.media)
dados.3$dados.dp <- as.numeric(dados.3$dados.dp)

Vejamos nosso resultado final executando o nome do nosso objeto dados.3.

dados.3

##    ano      local dados.media dados.dp
## 1 2020 Ambiente 1        14.1 2.846050
## 2 2020 Ambiente 2        13.1 1.286684
## 3 2021 Ambiente 1        13.0 1.581139
## 4 2021 Ambiente 2        14.8 1.934647

Pronto! depois de alguns (muitos) passos conseguimos construir nossa nova tabela com os dados resumidos.

É um processo longo porém necessário para se acostumar com o ambiente de trabalho e a linguagem R. Há caminhos mais rápidos e tão eficientes quanto. Que se tornam úteis quando lidamos com muitas categorias dentro de uma variável. Contudo para isso é necessário a instalação de algum pacote (Há vários pacotes que apresentam funções que permitem a realização deste processo de maneira mais rápida e eficiente). Vamos utilizar um exemplo começando pela instalação do pacote chamado Rmisc.

O comando abaixo realiza a instalação desse pacote. Conforme já fizemos com o pacote readxl.

install.packages("Rmisc")

Após instalado vamos carrega-lo pelo comando a seguir. Conforme já fizemos com o pacote readxl.

library(Rmisc)

Agora vamos conhecer a função summarySE() deste pacote o qual realiza os passos que fizemos anteriormente e ainda apresenta outros resultados. Mas iremos focar na média e desvio padrão.

resultado <- summarySE(data = dados, 
                       measurevar = "comprimento", 
                       groupvars = c("ano", "local"))
resultado

##    ano      local  N comprimento       sd        se        ci
## 1 2020 Ambiente 1 10        14.1 2.846050 0.9000000 2.0359414
## 2 2020 Ambiente 2 10        13.1 1.286684 0.4068852 0.9204382
## 3 2021 Ambiente 1  5        13.0 1.581139 0.7071068 1.9632432
## 4 2021 Ambiente 2 15        14.8 1.934647 0.4995236 1.0713715

Repare que a função summarySE() apresenta, basicamente, 3 argumentos, “data” que pede que se insira a planilha a ser utilizada, “measurevar” o qual pede a variável quantitativa que será sumarizada e “groupvars” o qual pede as variáveis categóricas¹¹ segundo as quais a variável mensurável será agrupada. Observe também que para esta função as variáveis devem ser colocadas entre aspas.

Pronto! Com a função summarySE() realizamos os mesmos passos que antes e guardamos o resultado dentro de um objeto chamado resultado. Repare que essa função nos resumiu os dados de comprimento de acordo com as duas variáveis categóricas que indicamos: ano e local. Em seu resumo ele nos forneceu, na seguinte ordem, as colunas: ano, local, N (número de observações), comprimento (média do comprimento), sd (desvio padrão), se (erro padrão) e ci (intervalo de confiança de 95%).

OBS: Este é um exemplo sobre a vantagem e importância de usar funções que estão presentes em outros pacotes.

Agora vamos usar o objeto resultado para desenvolver o gráfico de barras com o erro padrão (Figura 2.17). Porém para este caso, teremos que guardar nosso gráfico dentro de algum objeto, neste caso chamamos o objeto de grafico. Após o gráfico ser criado devemos utilizar a função arrows() que nos permite adicionar as barras de desvio padrão no nosso gráfico.

grafico <- barplot(formula = comprimento ~ ano + local,
                   data = resultado,
                   beside = TRUE,
                   col = c("red", "blue"),
                   ylim = c(0, 30),
                   ylab = "Comprimento médio (cm)",
                   legend.text = TRUE)
arrows(x0 = grafico,
       y0 = resultado$comprimento + resultado$sd,
       y1 = resultado$comprimento - resultado$sd,
       code = 3,
       angle = 90,
       length = 0.05)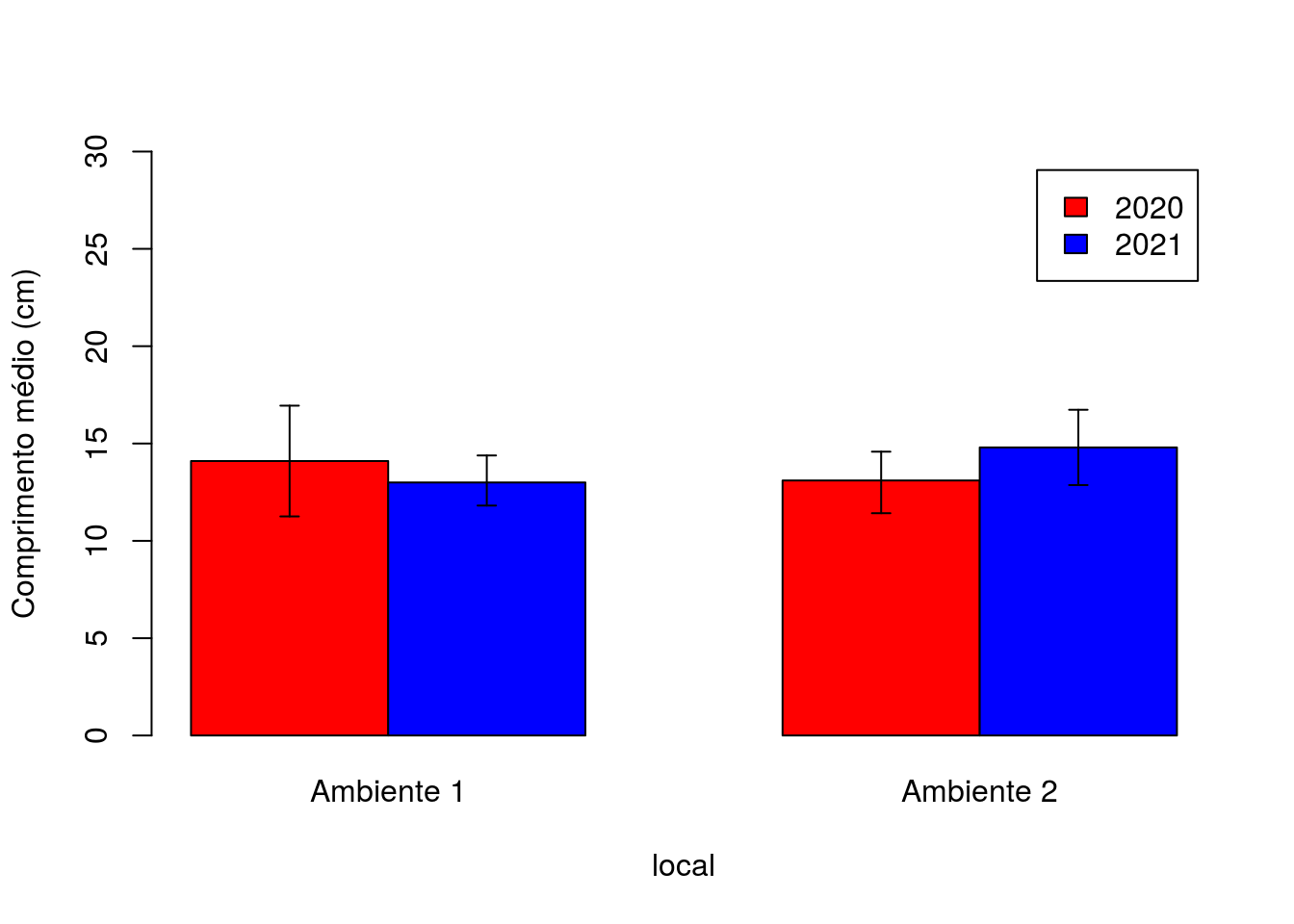

Figura 2.17: Gráfico de barras com erro padrão do comprimento por ano e local, da planilha resultado (derivada da planilha dados)

Note que na função barplot() utilizamos algumas mudanças em relação ao que fizemos anteriormente, como os argumentos “formula”¹² o qual indica a variável resposta em função das variáveis categóricas o qual será plotado (caso altere a ordem ano + local para local + ano a ordem do gráfico também será alterado. Teste você mesmo, veja o acontece). Neste caso, como temos mais de uma variável categórica adicionamos um argumento novo chamado “legend.text” o qual adiciona uma legenda ao gráfico.

A função arrows() que adicionou as barras de desvios no gráfico apresenta alguns argumentos diferentes do que já vimos em outros gráficos.

x0: o qual indica o objeto onde o gráfico foi armazenado;
y0: o qual é escrito como uma operação matemática onde devemos incluir o valor da média + coluna onde está a variável referente ao desvio;
y1: o qual é escrito como uma operação matemática onde devemos incluir o valor da média - coluna onde está a variável referente ao desvio;
code: determina o tipo de seta que será plotada;
angle: é o ângulo da haste da barra até a ponta;
length: é o comprimento das bordas da barra;

Terminamos de construir e entender os componentes do nosso primeiro gráfico com suas barras de erro.

O principal para construção desse gráfico consiste em entender como organizar os dados a serem graficados. Ao se usar a função barplot() para construção do gráfico de barras com os desvios, devemos ter uma ou mais colunas com as categorias, outra com os valores que desejamos e outra com os valores dos desvios.

Vamos realizar um segundo tipo de gráfico onde temos apenas uma variável categórica e seus respectivos desvios. Para isso utilizaremos nosso conjunto de dados abundancia (lembre-se que mes é uma variável categórica e deve ser identificada como fator) (Figura 2.18).

Neste conjunto de dados não precisamos reorganiza-los pois já se encontram organizados e já temos os valores dos desvios.

grafico <- barplot(abundancia$N,
                   ylim = c(0, 200),
                   xlab = "Mês",
                   ylab = "Abundância",
                   names.arg = abundancia$mes,
                   col = "green")
arrows(x0 = grafico,
       y0 = abundancia$N + abundancia$desvio,
       y1 = abundancia$N - abundancia$desvio,
       code = 3,
       angle = 90,
       length = 0.05)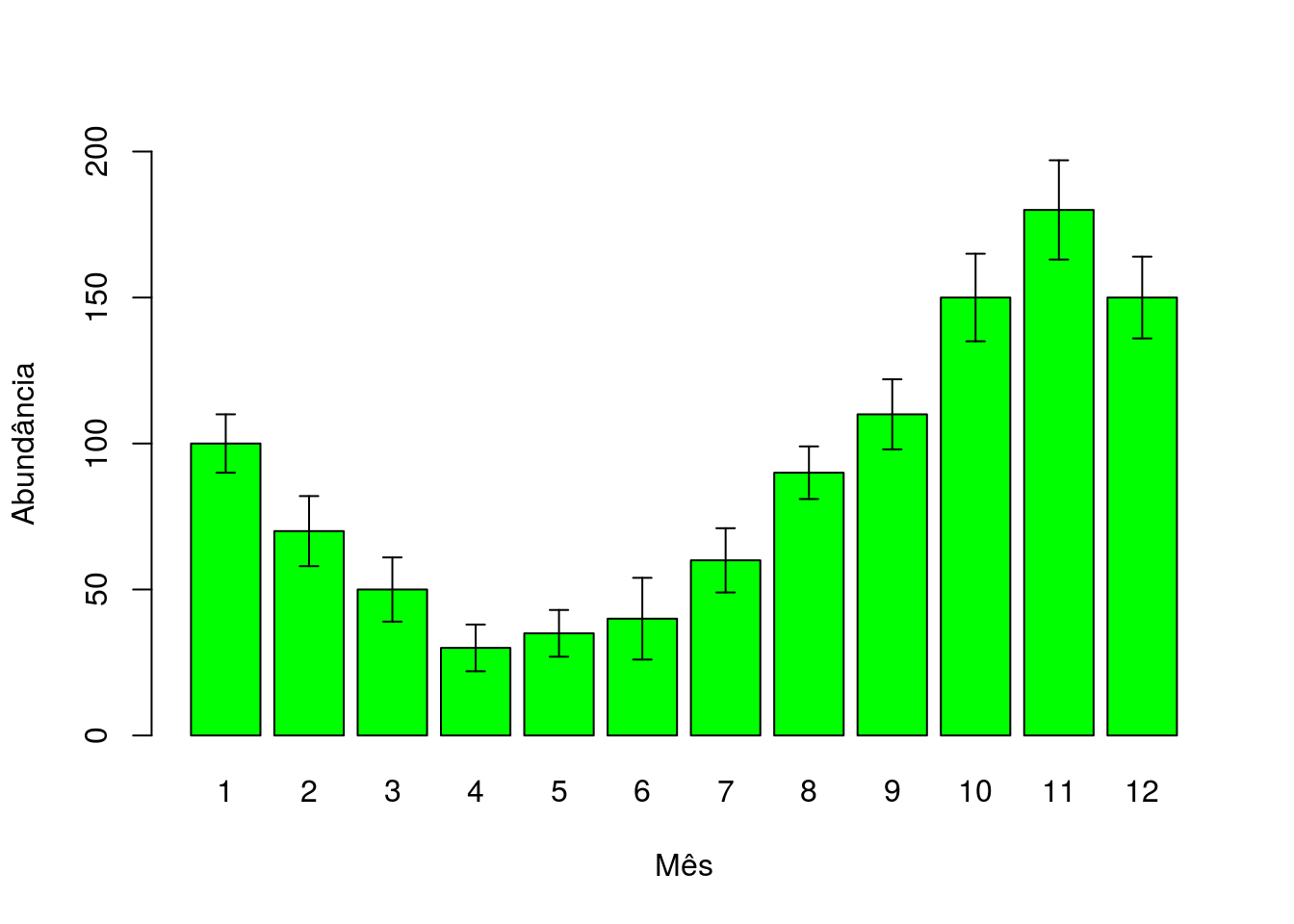

Figura 2.18: Gráfico de barras com erro padrão da abundância por mês da planilha abundância

Repare que é a mesma coisa que fizemos anteriormente,porém com outro conjunto de dados.

2.5 Considerações

Ao longo dos tópicos abordados neste capítulo demonstramos as etapas mais importantes e de diversos modos para nossa trajetória inicial e necessária no R, desde a definição do ambiente de trabalho, passando pela importação da planilha de dados, verificação e ajuste dos dados e sua sumarização gráfica e numérica (Figura 2.19).

Durante nosso percurso neste livro realizaremos mais gráficos aliados as análises estatísticas básicas comumente utilizadas. Não se assuste com a quantidade de etapas, funções, argumentos e nomes, eles irão se repetir tantas e tantas vezes daqui em diante que você não esquecerá. O aprendizado do R é exponencial e ele lhe permitirá entender como nunca o universo da análise de dados adequando-o para seu campo de atuação.

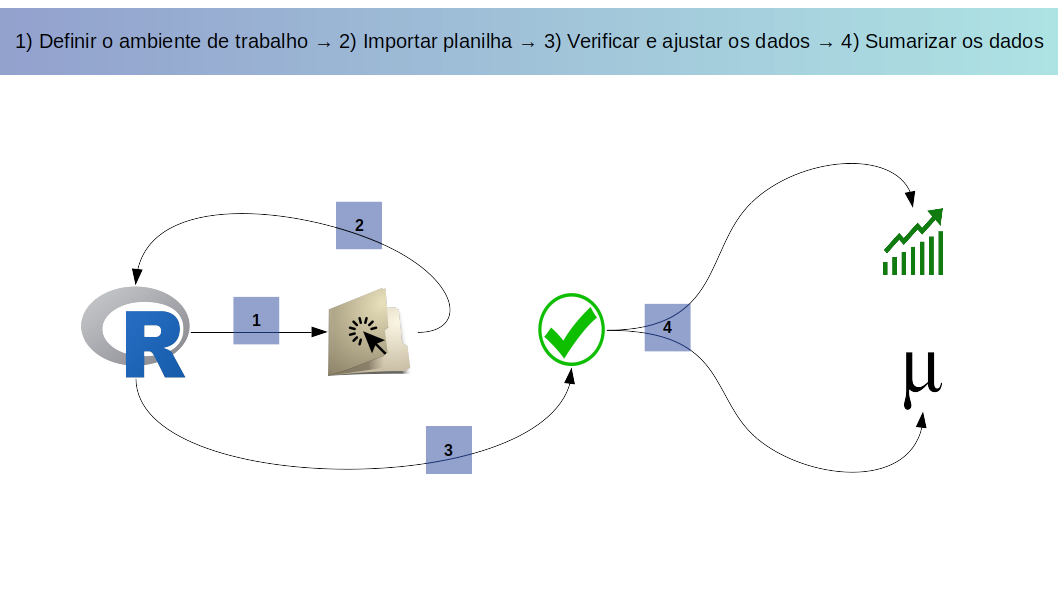
Figura 2.19: Resumo dos passos abordados no capítulo: da definição do ambiente de trabalho até a sumarização dos dados.

2.6 Exercícios

Para iniciarmos nosso trabalho no R precisamos saber importar os dados com os quais iremos trabalhar. Porém alguns passos são fundamentais antes da importação. Qual das opções a seguir contêm as funções, em ordem, que contemplam esses passos.

setwd(); choose.dir(); as.factor() e readxl()
setwd(); choose.dir(); readxl()
library(); setwd(); choose.dir()
choose.dir(); setwd(); library()
choose.dir(); setwd()

Ao importarmos nossos dados é importante saber a extensão em que os arquivos são encontrados (ex: *.csv ou *.xlsx). A função para importação dos dados é determinada pela extensão dos arquivos em que os dados se encontram. Qual as opções abaixo melhor apresenta os comandos responsáveis por importar um arquivo em *.csv e outro em *.xlsx?

read_csv(file = “dados.csv”, header = TRUE, sep = “,”); read.excel(path = “dados.xlsx”, col_names = TRUE)
read_csv(file = “planilha.csv”, header = TRUE, sep = “;”); read_excel(path = “planilha.xlsx”, col_names = TRUE)
read.csv(path = “planilha.csv”, header = TRUE, sep = “,”); read_excel(file = “planilha.xlsx”, col_names = TRUE)
read.csv(file = “dados.csv”, header = TRUE, sep = “;”); read_excel(path = “planilha.xlsx”, col_names = TRUE)
read.csv(file = “planilha.csv”, header = TRUE, sep = “,”); read.excel(path = “planilha.xlsx”, col_names = TRUE)

Durante o processo de importação dos dados é necessário checar se todas as variáveis foram entendidas pelo R como elas devem ser (ex. se determinada variável foi identificada como fator ao invés de numérico ou caracter). Para isso algumas funções são importantes para checar e alterar se necessário. Qual das opções abaixo indica as funções que permitem checar e alterar as variáveis, se necessário.

checar: View(), summary(); alterar: as.factor(), as.numeric(), as.data.frame()
checar: View(), str(); alterar: as.factor(), as.numeric(), as.integer()
checar: str(), as.data.frame(); alterar: as.data.frame(), as.numeric(), as.caracter()
checar: str(), summary(); alterar: as.caracter(), as.factor(), as.numeric()
checar: View(), as.data.frame(); alterar: as.integer(), as.numeric(), as.factor()

O R apresenta em alguns de seus pacotes conjuntos de dados que nos permitem fazer análises. Usando o conjunto de dados chamado iris, o qual pode ser carregado usando a função data(). Qual das opções abaixo apresenta o comando para gerar o gráfico apresentado?

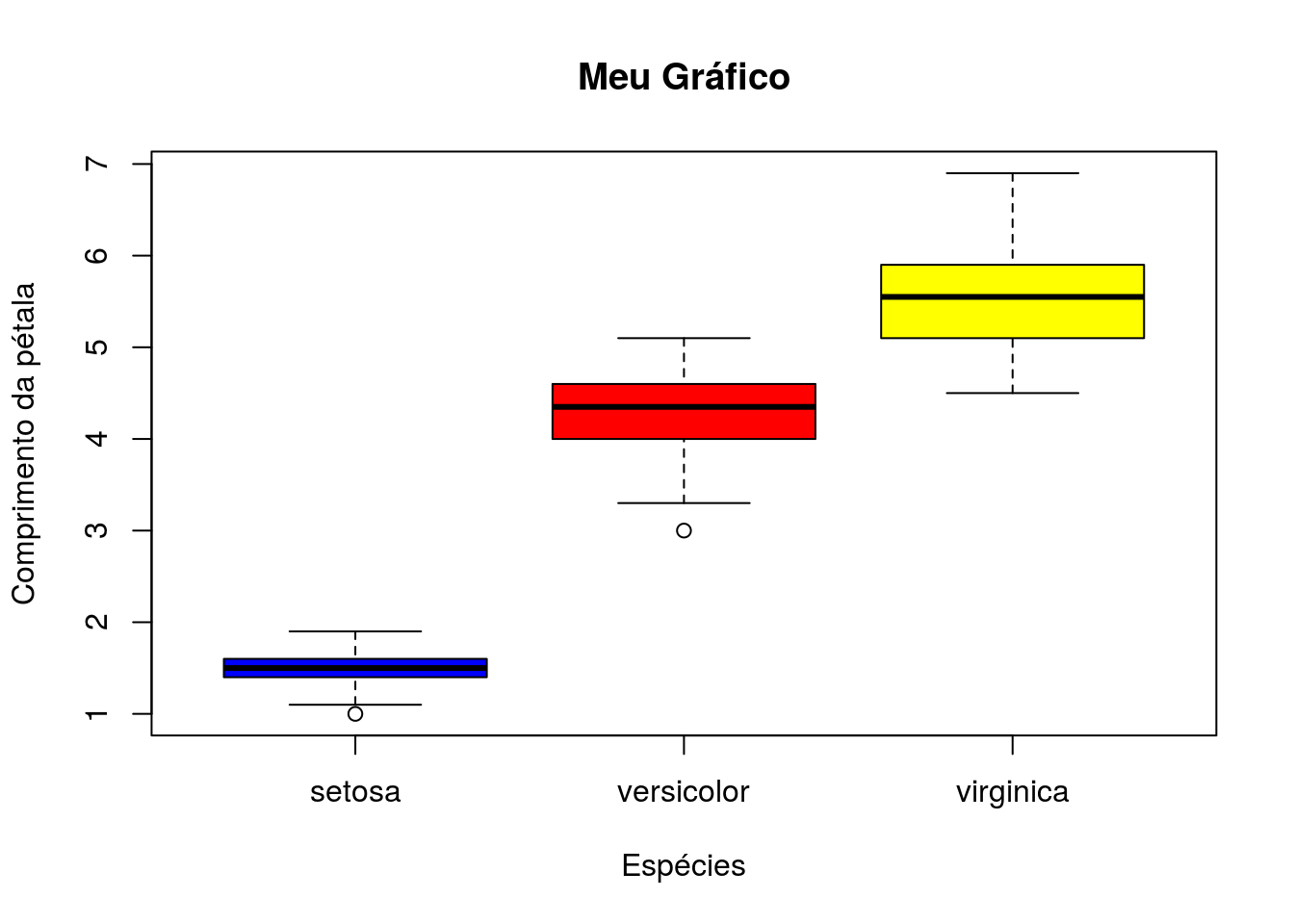
boxplot(Petal.Length, Species, data = iris, col = c(“blue”, “red”, “yellow”), xlab = “Espećies”, ylab = “Comprimento da pétala”, main = “Meu Gráfico”)
boxplot(Petal.Length ~ Species, data = iris, col = c(“blue”, “red”, “yellow”), xlab = “Espécies”, ylab = “Comprimento da pétala”, main = “Meu Gráfico”)
boxplot(“Petal.Length” ~ “Species”, data = “iris”, col = c(“blue”, “red”, “yellow”), xlab = “Espécies”, ylab = “Comprimento da pétala”, main = “Meu Gráfico”)
boxplot(Petal.Length ~ Species, data = iris, col = c(blue, red, yellow), xlab = “Espécies”, ylab = “Comprimento da pétala”, main = “Meu Gráfico”)
boxplot(Petal.Length ~ Species, data = iris, col = c(“azul”, “vermelho”, “amarelo”), xlab = “Espécies”, ylab = “Comprimento da pétala”, main = “Meu Gráfico”)

Execute os seguintes comandos no seu R: set.seed(458); teste <- rnorm(100, sd = 0.2). Qual das opções abaixo representam, na ordem, a média, mediana, desvio padrão, variância e amplitude destes dados.

0,01; 0,02; 0,12; 0,04; 1,24
0,02; 0,01; 0,21; 1,24; 0,04
0,02; 0,01; 0,21; 0,04; 1,24
0,01; 0,02; 0,12; 0,04; 1,24
0,02; 0,01; 0,31; 0,04; 1,20

Ver figura 1.6 ↩
Tudo que é realizado no R é por meio de comandos, esses comandos são compostos de funções, podemos reconhece-las pois logo após um nome que representa uma função obrigatoriamente há um parênteses e cada função apresenta argumentos, depois dos quais há o sinal de igual (=). As funções estão dentro de pacotes/bibliotecas, ou seja, cada biblioteca apresenta diversas funções e cada função diversos argumentos. O R, quando instalado, traz consigo alguns pacotes, mas estes pacotes não apresentam uma função que permite carregar arquivos *.xls ou *.xlsx. Portanto para que seja possível realizar essa tarefa devemos instalar, neste caso, o pacote readxl. Para instalação de pacotes podemos usar a função conhecida por install.packages(“nome do pacote”).↩
tibble e data frame são, em termos práticos para o livro, objetos similares↩
Aqui estamos representando como vírgula o separador decimal. Mas o R em seu resultado utiliza o ponto (.) como separador decimal. Pois por padrão ele está configurado para o sistema númerico inglês↩
Repare que usamos a função concatenar c() para agrupar as 2 variáveis categóricas de interesse.↩
similar a função boxplot.↩